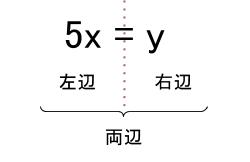
等号の左側を左辺、右側を右辺、両方をあわせて両辺といいます。
等式
等号で結ばれた式を等式といいます。
たとえば、
たてが \( x\) \(cm\)、よこが \( 5\) \(cm\) の長方形の面積は、 \( y\) \( cm^2\) である。
これを式を用いて表現すると、
\( 5x=y\)
となります。
このような、等号で結ばれた式を等式といいます。
他にも
\(2+3=5 \)
\(15=5×3\)
\(2a+3b=5\)
これらも等式です。
等号の左と右が等しいよ、ということを表す式のことです。
等号の左側を左辺、右側を右辺、両方をあわせて両辺といいます。
等式で数量関係を表す
\(2\) つの数量が等しい、ということを等式で表すことで、
様々な計算処理が可能になります。
文章から等式を作る練習をしましょう。
(1)\(1000\) 円を出して、\(1\) 個 \(x\) 円の鉛筆 \(4\) 本を買うとおつりは \(720\) 円だった。
これを等式で表すと
\(1000-4x=720\)
(2)\(x\) 枚の紙を \(y\) 人の子どもに \(4\) 枚ずつ配るには、\(7\) 枚足りない。
これを等式で表すと
\(x+7=4y\)
※等式は他の表記でも可能です。
例えば(2)は、\(\displaystyle \frac{x+7}{4}=y\) なども可能です。
他にもいくらでも別表記が可能です。
例題
次の数量の関係を、等式で表しなさい。
(1)ある数 \(x\) の \(3\) 倍から \(4\) を引くと、\(x\) の \(2\) 倍よりも \(5\) 大きくなる。
(2)\(a\) mの長さのロープを、\(4\) 人で等分したところ、\(1\) 人分のテープの長さは \(b\) mになった。
(3)\(60\) を \(a\) で割ったら、商が \(3\) で、余りが \(b\) であった。
(4)\(12km\) の道のりを、時速 \(a\) kmで進むと、\(b\) 時間かかった。
解説
(1)ある数 \(x\) の \(3\) 倍から \(4\) を引くと、\(x\) の \(2\) 倍よりも \(5\) 大きくなる。
これは、文章をそのまま式にするだけと言えます。
\(3x-4=2x+5\)
これが求める等式です。
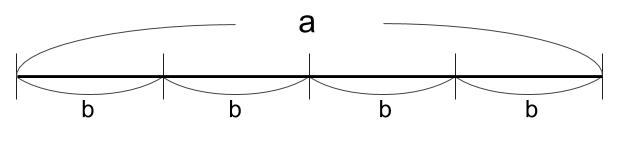
(2)\(a\) mの長さのロープを、\(4\) 人で等分したところ、\(1\) 人分のテープの長さは \(b\) mになった。
つまり、割り算ですから、
\(a÷4=b\)
ということです。
ただし、文字式の世界に÷は用いませんから、
分数で表現します。
つまり、
\(\displaystyle \frac{a}{4}=b\)
これが求める等式です。
もちろん、
\(a=4b\)
でも正解です。
(3)\(60\) を \(a\) で割ったら、商が \(3\) で、余りが \(b\) であった
割り算ですね。
\(60÷a=3 あまり b\)
当然ですが、文字式の表現に、「÷」も「あまり」もありません。
割り算を、線分図でとらえる訓練をしましょう。
下図のようになります。
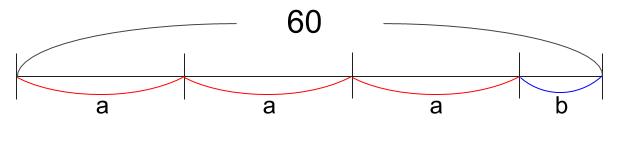
つまり、
\(60=3a+b\)
これが求める等式です。
(4)\(12km\) の道のりを、時速 \(a\) kmで進むと、\(b\) 時間かかった
いわゆる速さの \(3\) 公式に従えば、
\(3\) 通りの等式が可能です。
単位に気を付けて等式にします。
速さ×時間=距離
\(ab=12\)
距離÷時間=速さ
\(12÷b=a\)
つまり、
\(\displaystyle \frac{12}{b}=a\)
距離÷速さ=時間
\(12÷a=b\)
つまり、
\(\displaystyle \frac{12}{a}=b\)
\(3\) 通りの等式が可能です。
実は他の問題も、別解を何通りか作ることができます。
スポンサーリンク
