【中学数学】移項と様々な１次方程式

移項

前回学習した超重要事項、等式の変形ですが、
この式操作から、「移項」という重要計算技術を得ます。

具体例で見ていきましょう。

\(x+8=12\)
これを等式の変形を用いて解きます。

４つの等式が並んでいましたが、2つ目の式を省略すると
以下のようになります。
下線部分に注目です。

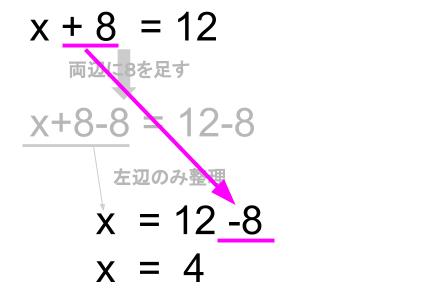
まるで、左辺の \(+8\) が右辺に符号を変えて \(-8\) となって移動したように見えます。
この操作を「移項」と読びます。
他方の辺からもう一方の辺へ、項を符号を変えて移動することです。

移項とは、上で見たように等式の変形から導かれることです。
等式の変形を１ステップ省略したものともいえます。

等式を線分図でとらえると・・・

\(x=y+3\) という等式があります。

これを線分図で視覚化してみます。

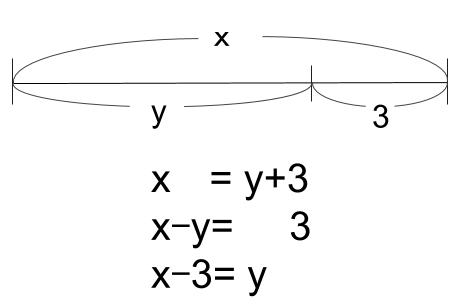
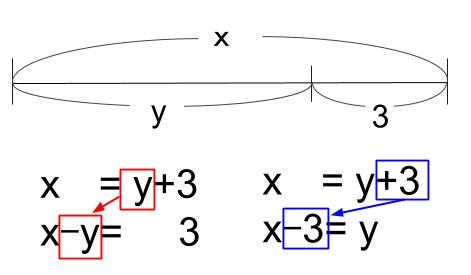
この図を見ればわかるとおりですが、
\(x=y+3\)
を表したこの図は、
\(x-y=3\)
や
\(x-3=y\)
を表しているともいえます。

移項が成り立っていることが、視覚的にも確かめられますね。

移項によって、方程式を解く

方程式を解くとは、等式の変形を上手に行って、
\(x=\)数値
というところまで式変形をすることです。
そのさい、移項を用いて、
式変形の手間を少しだけ減らすことができます。

方程式の解き方をまとめます。

1. 移項によって、左辺に \(x\) の項を集める
2. 移項によって、右辺に数の項を集める
3. 両辺を \(x\) の係数で割る

この手順で、方程式を解くことができます。

例題

次の方程式を解きなさい。
（１）\(-3x=10+2x\)
（２）\(4x-7=9x+8\)

解説

（１）

\(x=-2\)
（２）

\(x=-3\)

スポンサーリンク

• 次のページ １次方程式の解法・決定版
• 前のページ 等式の変形