比例・水そう
水そうに一定の割合で、水を入れていく問題は、
比例の定番中の定番です。
例題1
\(32L\) の容積の水そうに毎分 \(4L\) ずつ水を入れていく。水を入れる時間を \(x\) 分 、
その間に入る水の量を \(yL\) とします。\(x\) と \(y\) との関係について、次の問いに答えなさい。
(1)\(y\) を \(x\) の式で表しなさい。
(2)\(x,y\) の関係をグラフで表しなさい。
(3)\(x\) の変域と \(y\) の変域を求めなさい。
(4)\(25L\) 入れるためには何分間必要か求めなさい。
解説
(4)\(25L\) 入れるための時間
小学生なら、(1)から(3)は意味不明ですが、
(4)が解けますね。
\(25÷4=\displaystyle \frac{25}{4}\)
よって、\(\displaystyle \frac{25}{4}\) (分)
と求まります。
(1)\(y\) を \(x\) の式で表しなさい。
この問題では、
\(1\) 分で \(4L\)
\(2\) 分で \(8L\)
\(3\) 分で \(12L\)
\(4\) 分で \(16L\)
と規則正しく水が入ります(比例です)。
\(y\) 分で \(xL\) という \(2\) 量の関係は、
明らかに、 \(y=4x\) という関係式になっています。
答えは、 \(y=4x\) です。
(2)と(3)を同時に解決
満水になるのは、当然、\(32÷4=8\) より、
\(8\) 分で \(32L\) の満水です。
つまり、「(3) \(x\) の変域と \(y\) の変域」が求まりましたね。
\(0 \leqq x \leqq 8\)
\(0 \leqq y \leqq 32\)
です。
これらをもとに、グラフをかきます。
グラフのための目盛りが、
右 \(1\) 目盛りは \(1\) 分
上 \(1\) 目盛りは \(2L\)
であることをまず読み取ります。
そして、
\(1\) 分で \(4L\)
\(2\) 分で \(8L\)
\(3\) 分で \(12L\)
\(4\) 分で \(16L\)
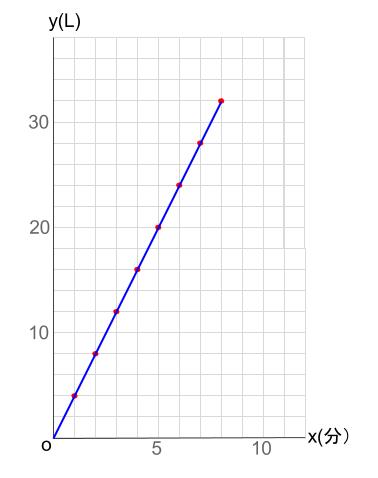
と点を取っていきます。
\(8\) 分で \(32L\) までです。
これらを直線で結べばグラフの完成です。
比例・速さ
一定の速さで、進む問題も、比例の定番中の定番です。
例題2
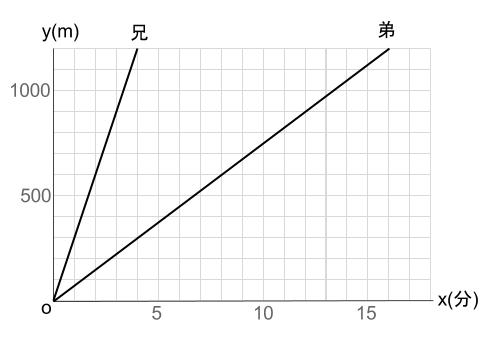
兄は自転車に乗って、弟は徒歩で、家を同時に出発し、家から \(1200m\) 離れた駅に向かった。出発から \(x\) 分後に、家から \(ym\) 離れた地点にいるとき、\(2\) 人の進行の様子
は下のグラフのようになった。次の問いに答えなさい。
(1)兄について、\(y\) を \(x\) の式で表しなさい。
(2)弟について、\(y\) を \(x\) の式で表しなさい。
(3)家を出発してから \(9\) 分後に、弟は家から何mの地点にいたか求めなさい。
解説
(1)兄について、\(y\) を \(x\) の式で表しなさい。
兄は、\(1200m\) を \(4\) 分かけて進んでいるので、
\(1\) 分で \(300m\) 進みます。
よって、 \(y=300x\) です。
あるいは、直線の傾きに注目すれば下図のようになります。
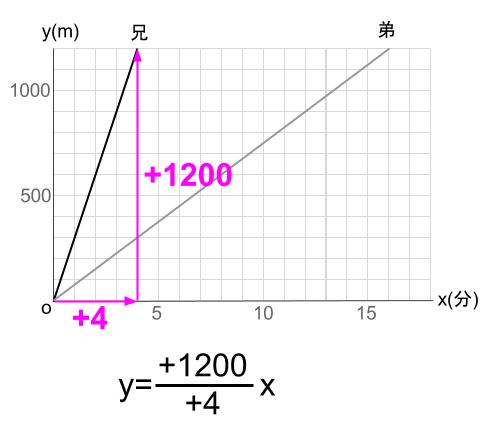
※本質的には同じ解き方をしています。
(2)弟について、\(y\) を \(x\) の式で表しなさい。
兄は、\(1200m\) を \(16\) 分かけて進んでいるので、
\(1\) 分で \(75m\) 進みます。
よって、 \(y=75x\) です。
あるいは、直線の傾きに注目すれば下図のようになります。
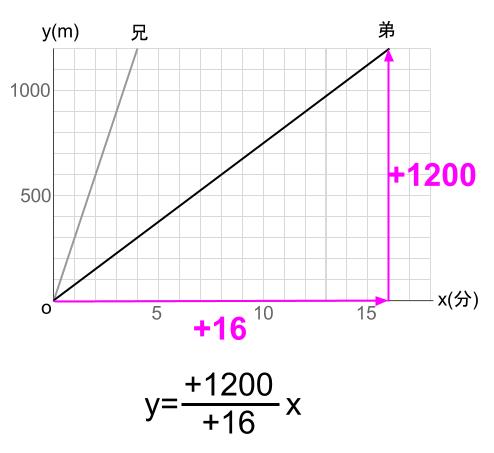
※本質的には同じ解き方をしています。
(3)家を出発してから \(9\) 分後に、弟は家から何mか
グラフを見ても、格子点ではないので読み取れませんね。
(2)で求めた弟の式を使います。
\(y=75x\)
なので、この式に \(x=9\) を代入します。
\(y=75×9\)
より
\(y=675\)
よって、\(675m\) です。
※もちろん、弟の速さが、分速 \(75m\) なので、
\(75×9=675(m)\) と解いてもOKです。
スポンサーリンク
