比例
空の水そうに、毎分 \(2L\) ずつ水を入れていく。水を入れはじめてから \(x\) 分後の、水そう内の水量を \(yL\) とする。 \(x\) と \(y\) の関係を表にまとめると以下のようになる。
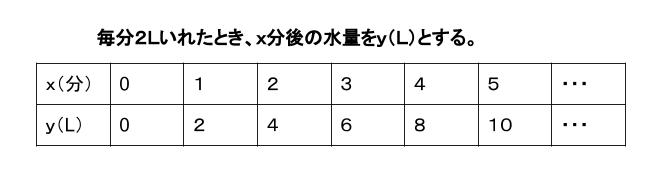
\(y\) は常に \(x\) の \(2\) 倍であるので、 \(y\) と \(x\) の関係は、\(y=2x\) という式にまとめることができます。

このように、 \(x\) と \(y\) の関係が
\(y=ax\)( \(a\) はなんらかの数、ただし \(0\) ではダメ)
となるとき、
\(y\) は \(x\) に比例するといいます。
\(a\) を比例定数といいます。
定数とは、「定まった数」という意味です。今回の例ならば、\(a=2\) です。
それに対して、
\(x\) と \(y\) は、いろいろな値をとります。
このような文字を変数といいます。
比例の性質確認
比例の性質
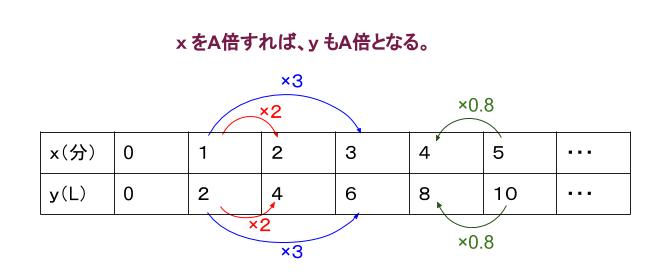
比例では \(x\) が \(2\) 倍、\(3\) 倍、\(4\) 倍・・・になると、 \(y\) も \(2\) 倍、\(3\) 倍、\(4\) 倍・・・になります。
比例する関係の具体例
ずいぶんと堅苦しく比例の話をしてきましたが、
比例は小学校のころから何度も扱ってきたものです。
\(1\) 個 \(30\) 円のガムがあります。
\(2\) 個 \(60\) 円,
\(3\) 個 \(90\) 円,
\(4\) 個 \(120\) 円,
となりますね。
ただこれだけです。
比例とはただこれだけのことです。
難しく考えないでください。
このガムを \(x\) 個買うときの値段を \(y\) 円としたとき、
\(y=30x\) となります。
比例する量をこのように式で表すと、
\(y=ax\) の形になります。
例題
\(20\) 枚の重さが \(30g\) の同じ大きさの紙があります。
次の問いに答えなさい。
(1) \(x\) 枚のときの重さを \(yg\) として、\(x\) と \(y\) の関係を式で表しなさい。
(2) この紙 \(36\) 枚では何\(g\) になりますか。
(3) この紙の重さが \(75g\) のときの紙の枚数を求めなさい。
解説
(2)と(3)だけなら、小学生で学習済の問題ですね。
\(1\) 枚の重さが \(30÷20=1.5\)\((g)\)
\(2\) 枚の重さが \(3g\)
\(3\) 枚の重さが \(4.5g\)
\(4\) 枚の重さが \(6g\)
以下同様に続く。
つまり、枚数と重さが比例していることに気付けますね。
(1)を飛ばして、(2)(3)を回答することもできますが、
(1)から順に見ていきましょう。
(1)\(1\) 枚の重さが \(1.5g\) ですから
\(x\) 枚のときの重さ \(y\) は、\(1.5x\)
よって、\(y=1.5x\)
(2)(1)で求めた式に、\(x=36\) を代入します。
\(y=1.5×(36)\)
\(y=54\)
よって、\(54g\) です。
(3)同様に、(1)で求めた式に、\(y=75\) を代入します。
\(75=1.5x\)
\(x=50\)
よって、\(50\) 枚です。
変域
はじめの水そうの例 \(y=2x\) で、水を入れ始めてから \(6\) 分後に、水そうが満水になったとします。
この場合、\(x=7\) とか、\(x=6.01\) という値をとることはありません。
つまり変数 \(x\) は、\(0\) 以上 \(6\) 以下のいずれかです。
それに応じて、変数 \(y\) の値の取りうる範囲は、\(0\) 以上 \(12\) 以下となります。
このように、変数のとりうる値の範囲を、その変数の変域といいます。
●変域は不等号を用いて表します。
●変域は数直線で表すとわかりやすい。
①「~以上」、「~以下」は、その数も含みます
\(x\) が \(0\) 以上 \(6\) 以下のとき、 \(x\) は \(0\) や \(6\) であってもOKです。
これを不等号で以下のように表します。
\(0 \leqq x \leqq 6\)
また数直線でも表します。黒丸は、その数を含むという表現です。

②「~より大きい」、「~より小さい=未満」 は、その数も含みません。
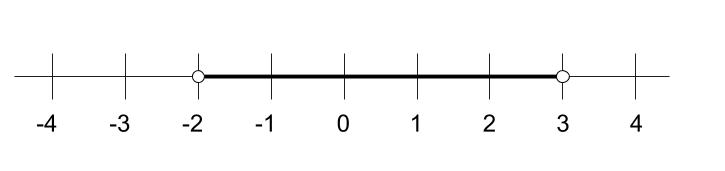
\(x\) が \(-2\) より大きく、\(3\) 未満のとき、 \(x\) は \(-2\) や \(3\) ではいけません。
これを不等号で以下のように表します。
\(-2 \lt x\lt 3\)
また数直線でも表します。白丸は、その数を含まないという表現です。
比例のグラフ
さて、比例はグラフとして表すことも、小学生のときに学習していますね。
\(x\) や \(y\) を用いた文字式を使わなかっただけです。
さきほどの水そうの例を、グラフにしてみましょう。
\(1\) 分間に \(2L\) ずつ、空の水そうに水を入れます。
水を入れ始めてから \(6\) 分で満水になったとします。
入れ始めてから \(x\) 分後の水量を \(yL\) とすると、以下の表のようにまとめられます。
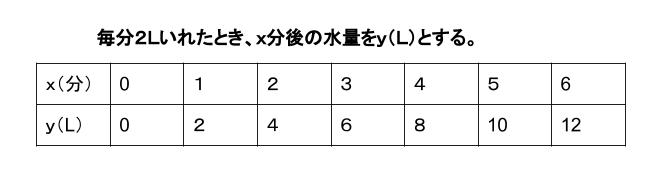
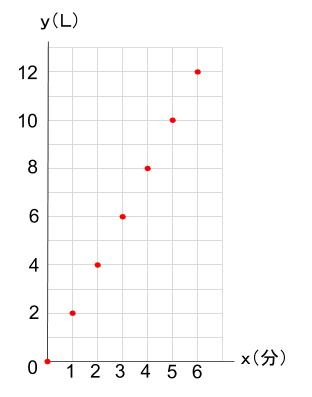
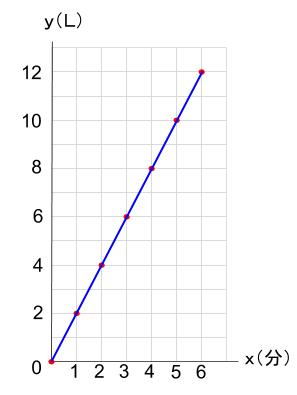
この \(7\) つを点にとり、それを結べばグラフとなります。
時間の経過とともに、水量が増えていく様子をうまく表すことができています。
\(x\) が整数のとき以外、つまり水を入れ始めてから \(2.3\) 分後などもあるわけですからね。
以上は、小学生のときにも学習したものの復習となります。
このように \(2\) 量の関係(時間と水量)は、平面の中で \(1\) つの点として表現することができます。
その点が集まったものが、比例のグラフであり、直線になります。
スポンサーリンク
