例題
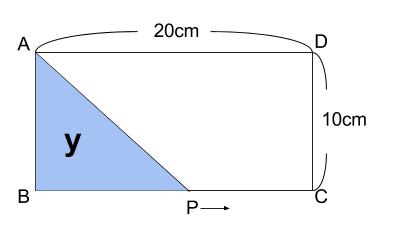
下の図の長方形 \(ABCD\) の辺上を、点 \(P\) が点 \(B\) を出発し点 \(C\) まで、\(1\) 秒間に \(2cm\) の一定の速さで動きます。点 \(P\) が出発してから \(x\) 秒後の三角形 \(ABP\) の面積を \(ycm^2\) とします。次の問いに答えなさい。
(1)\(y\) を \(x\) の式で表しなさい。
(2)\(x\) の変域を求めなさい。
(3)\(y\) と \(x\) の関係を表すグラフをかきなさい。
解説
動点の問題は、一度じっくりと向き合って、完璧に理解することが重要です。
そして、ポイントをつかんでさえしまえば、
今後はスラスラと解くことができるようになります。
とにかく一度、じっくりとゆっくりと、完璧な理解を目指しましょう。
まず、この問題で何が起こっているのか、何が問われているのか、を把握しましょう。
点 \(P\) が出発してから、\(1\) 秒後、\(2\) 秒後、\(3\) 秒後・・・と図示してみましょう。
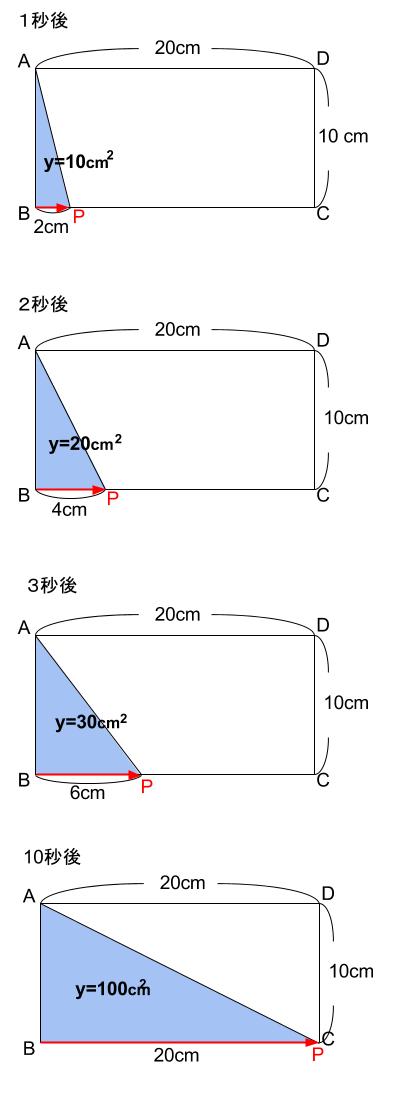
\(P\) が時間とともに、右に移動していき、三角形 \(ABP\) の面積がどんどん増えていっている様子がわかります。\(10\) 秒後、点 \(C\) につくまでをグラフに表してみましょう。
グラフをかくのは(3)ですが、そんな順番なんて関係ありません。どんどんグラフをかいてしましましょう。\(x=0\) のとき、\(y=0\) もあたりまえですね。
これらの点は、直線で結んでしまってよいですね。
つまり、三角形 \(ABP\) の面積は、一定の割合で増加しているということです。
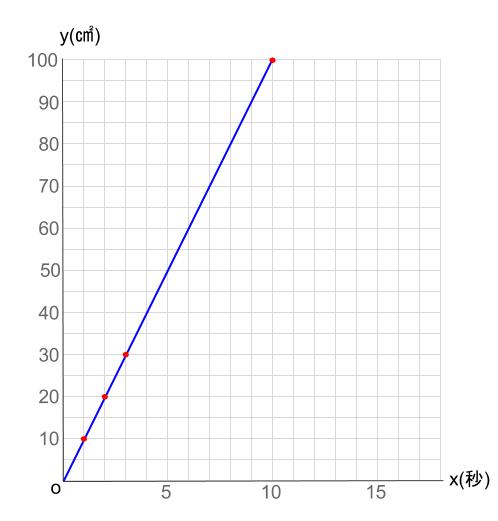
この直線の式を求めれば、これが(1)の答えになります。
\(1\) 秒で \(10cm^2\) ずつ増えるグラフなので、\(y= 10x\)
と求まりました。
当然 \(x\) の変域は、
\(0 \leqq x \leqq 10\)
です。
以上、(1)から(3)が解決しました。
別解
ちなみに、次のような解法もあります。とても大事ですので必ずこちらも理解しておいてください。
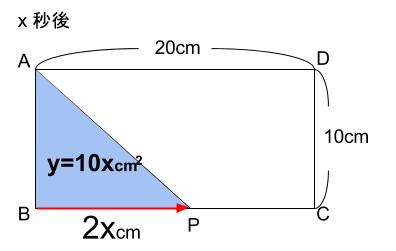
\(x\) 秒後の三角形 \(ABP\) の底辺は、\(2xcm\) なので、
このときの 面積 \(y\) は、底辺×高さ÷2の公式より、
\(y=2x×10÷2=10x\)
グラフから得た式と、まったく同じ式が得られましたね。
スポンサーリンク
