比例のグラフをかく
\( y=2x\) の式を満たす、\(x,y \) の組は
\((0,0)\)、\((1,2)\)、\((2,4)\)、\((3,6)\)・・・などであり、
これらの点を結べば、比例のグラフの完成となりました。
今回は、上記の基礎事実をふまえた上で、
比例のグラフの書き方をさらに深く学んで行きましょう。
たった2点で直線は決まる
例題1
次の式のグラフをかきなさい。
\( y=-2x\)
解説
\( y=-2x\) の式を満たす \(x,y \) の組は
\((0,0)\)、\((1,-2)\)、\((2,-4)\)、\((3,-6)\)、\((4,-8)\)・・・などです。
これらの点を結べば比例のグラフが完成するわけですが・・・
実は、直線が通る座標は、たった \(2\) 点あれば十分です。
\(2\) 点を通る直線は、ただ \(1\) つに定まるからです。
よって、\( y=-2x\) の式を満たす、\(x,y \) の組は
\((0,0)\)、\((1,-2)\) の \(2\) 点で十分です。
あとは、この \(2\) 点を通る直線を引けば完成です。
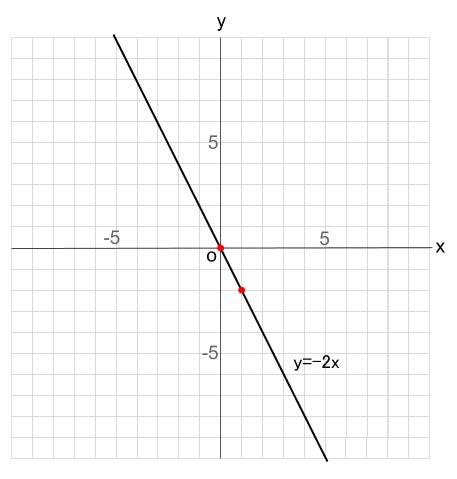
たった \(2\) 点で直線はかける!
という論理的には正しい話をしましたが、実際に作図をするときには要注意です。
\((0,0)\)、\((1,-2)\) の \(2\) 点を通るように定規をあて、直線を書くわけですが、
書いた直線が、本来通るべき座標、例えば \((-5,10)\) からずれてしまうこと
はよくあることです。
通るべき格子点( \(x\) 座標も \(y\) 座標も整数の点)からずれてしまうと、
テストで減点されたり、×(バツ)になったりしますので、注意が必要です。
直線の傾き
直線を確定させるには、たった \(2\) 点で十分という論理はともかく、
実際にグラフを書く際には、直線が通る格子点に注意する必要があります。
結局たくさんの座標を求めるという話なのですが、その座標の求め方には別のアプローチもあります。
直線が、どのように進んでいくのか、に着目するのです。
もっと具体的に言うと、
「 \(x\) 方向に \(a\) 進む間に、\(y\) 方向に \(b\) 進む」という進み方に着目するのです。
\( y=-2x\) ですと、
「 \(x\) 方向に \(1\) 進む間に、\(y\) 方向に \(-2\) 進む」
となります。
これは、直線を坂道と見立てた時の、坂道の傾き具合を表しています。
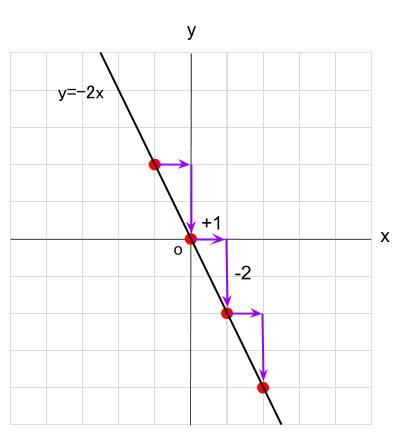
この比喩の通り、比例の式、\( y=ax\) における比例定数 \(a\) のことを、直線の傾きとも言います。
※これは中学2年の「 \(1\) 次関数」で正式に習うことが多いようですが、この段階から学習していましましょう。
変化の割合とも呼ばれます。
比例のグラフは必ず原点 \((0,0)\) を通るので、
あとはこの直線の傾きにしたがって進んでいけばよいのです(あるいは戻っていけばよい)。
右に \(1\) 進み、下に \(2\) 進む。
これのくり返しです。
比例定数を分数にする
例題2
次の式のグラフをかきなさい。
\( y=\displaystyle \frac{2}{3}x\)
解説
さて、この式のグラフはどのようになるのか。
まず、比例の式は必ず原点 \((0,0)\) を通ります。
次に、どのような座標を通るのか考えます。
\(x\) 座標、\(y\) 座標ともに整数になる格子点でないと作図できませんので・・・
\(x=3\) のとき、\(y=2\) になることがすぐに見つかりますね。

あとは、この
右に \(3\) 進み、上に \(2\) 進む
のくりかえしです。
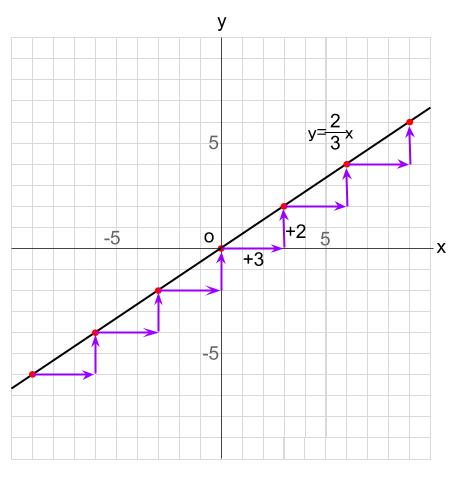
比例定数=傾き が表すもの
\(y=-2x\) ですと、
「 \(x\) 方向に \(1\) 進む間に、\(y\) 方向に \(-2\) 進む」
\( y=\displaystyle \frac{2}{3}x\)
「\(x\) 方向に \(3\) 進む間に、\(y\) 方向に \(2\) 進む」
右に \(3\) 進み、上に \(2\) 進む
それぞれの比例の式が、この坂道の特徴を決めているわけです。
当然ですが、比例定数がこの坂道を上り坂にするか、下り坂にするか、
急な道にするか、緩い道にするか、を決めています。
比例定数 \(a\) を分数で表し、 \( a=\displaystyle \frac{Q}{P}\) とすると、
\( y=\displaystyle \frac{Q}{P}=\displaystyle \frac{y座標の変化量}{x座標の変化量}\)
となります。
進行方向を右向き( \(x\) 座標の正の方向)とし、必ず分母を正にすると、
右に \(P\) 進む間に、\(y\) の変化量 \(Q\) が正ならば上り坂、\(y\) の変化量 \(Q\) が負ならば下り坂であることがわかります。

比例定数=傾きが
正なら上り坂
負なら下り坂
になることが分かります。
変域のある比例のグラフ
例題
\(y=-x\) (\(-2 \leqq x \leqq 3\))
解説
変域がある以外は、今まで同じです。
まず、比例定数\(-1=\displaystyle \frac{-1}{1}\) とします。
つまり、右に \(1\) 進む間に、下に \(1\) 進む下り坂です。
あとは、変域、\(-2 \leqq x \leqq 3\) の範囲でグラフをかけば終了です。
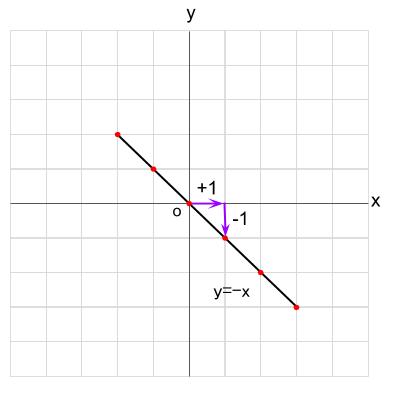
スポンサーリンク
