グラフの読み取り
比例のグラフが与えられ、そこから問題がはじまることもよくあります。
グラフの読み取りを練習しましょう。
例題1
下の比例のグラフについて次の問いに答えなさい。
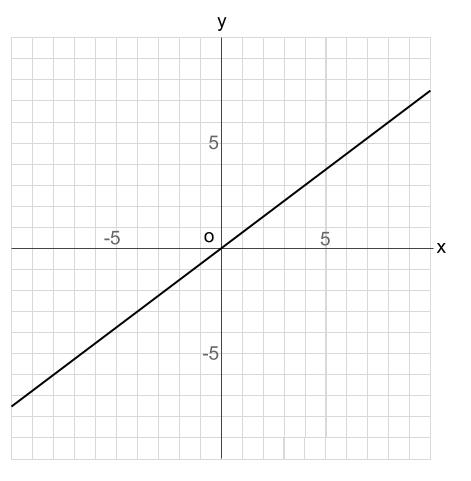
①このグラフの式を求めなさい
②\(x\) の値が \(3\) のときの \(y\) の値を求めなさい。
解答
①グラフの式
グラフのかき方を学習した今、この問題は難しくありませんね。
まずは、\(x\) 座標、\(y\) 座標がともに整数である、格子点を探しましょう。
もちろん直線が通っている格子点です。
\((4,3)\) が見つかります。
他の格子点を見つけてもかまいません。
\((8,6)\),\((-4,-3)\) などありますね。
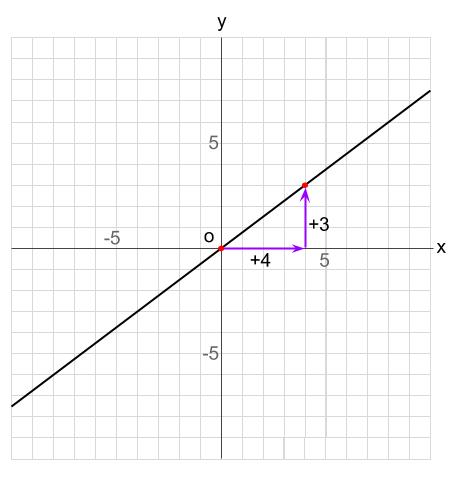
これは、比例定数を表していますね。
\(x\) の増加量を分母に、
\(y\) の変化量(増加も減少もありうる)を分子にすると、
比例定数が求まります。
よって、\(y=\displaystyle \frac{3}{4}x\) となります。
②\(x\) の値が \(3\) のときの \(y\) の値
グラフから読み取ることはできませんが、①で求めた式から計算できます。
\(y=\displaystyle \frac{3}{4}x\)
に \(x=3\) を代入します。
\(y=\displaystyle \frac{3}{4}x×3=\displaystyle \frac{9}{4}\)
となります。
例題2
下の比例のグラフの式を求めなさい。
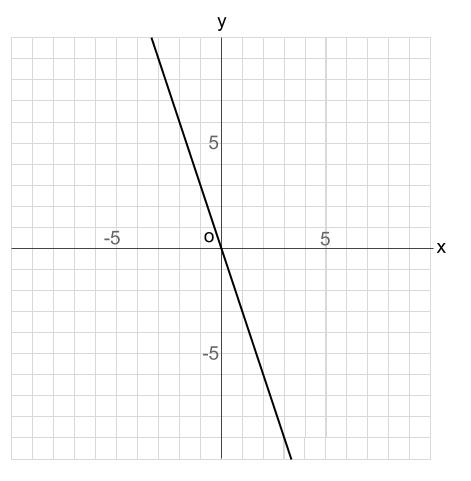
解答
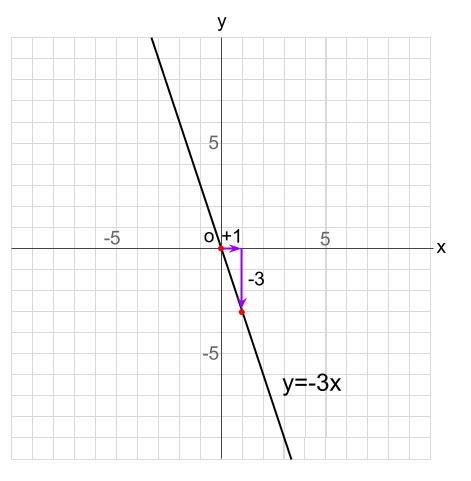
\(x\) が \(1\) 増える間に、 \(y\) は \(3\) 減っています。
つまり、この直線の傾きは \(\displaystyle \frac{yの増加量}{xの増加量}=\displaystyle \frac{-3}{+1}=-3\) です。
より、求めるグラフの式は、
\(y=-3x\) です。
スポンサーリンク
