【中学数学】座標平面

座標平面

中学生の数学では、座標平面という平面上に比例のグラフをかきます。
※中学 $2$ 年、$3$ 年と学習を進めていくと、比例以外のグラフもかいていきます。

小学校のときとの大きな違いは、 $y$ や $x$ が負の数のときまで考えるということです。

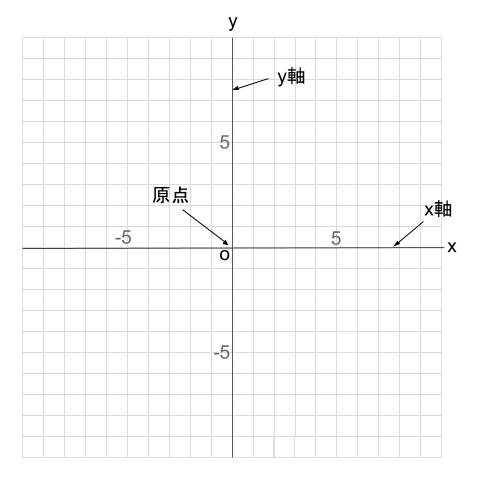
座標平面とは下のようなものです。

横の数直線を $x$ 軸
たての数直線を $y$ 軸
$2$ つの数直線が交わる点を原点といい、$O$ （アルファベットのオー）で表します。
原点はたて、よこの数直線がともに $0$（ゼロ）である点です。

$中学数学・高校受験chu-su-　座標平面　図１$

この座標平面を用いると、平面上のすべての点を $2$ つの数字の組合せで表すことができます。
原点からみて、

この $2$ つの情報で、平面上の位置がたった $1$ つに定まります。

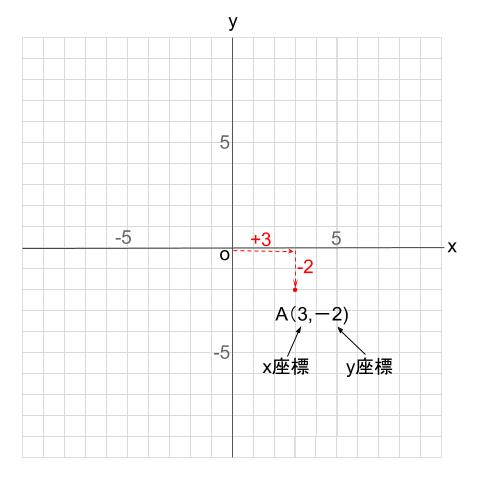
例えば、$x$ 軸方向に $3$、 $y$ 軸方向に $-2$ 進んだ位置にある点 $A$ を、
$A(3,-2)$
のように表します。
これを座標といいます。

$中学数学・高校受験chu-su-　座標　図$

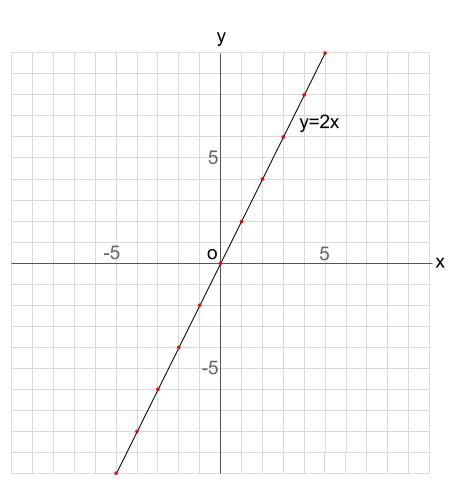
座標平面に $y=2x$ のグラフをかいてみましょう。
時間とか水量などと一切関係がないただの式、 $y=2x$　をグラフにします。
ただの数式なので、変域を考えないでかきます。
つまり、$x$ や $y$ のとる値に制限はありません。

$y=2x$
この式を満たす、$x$ と $y$ の組を座標とし、その線を結ぶことでグラフとなります。
通る座標は
$(-1,-2)$
$(0,0)$
$(1,2)$
$(2,4)$
などです。

もちろん、$(0.1,0.2)$ のような座標も通っています。
$y=2x$ のグラフは、無限の点の集合と言えます。

$中学数学・高校受験chu-su-　ｙ＝２のグラフ$