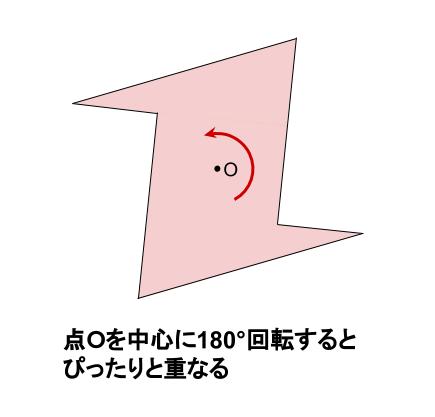
点対称な図形
\(1\) つの点を中心として \(180°\) 回転するとき、もとの図形にぴったりと重なる図形を
点対称な図形といいます。
中心となる点を対称の中心といいます。
対応する点、角、辺
\(180°\) 回転してぴったりと重なる辺、点、角を、それぞれ、
対応する辺
対応する点
対応する角
といいます。
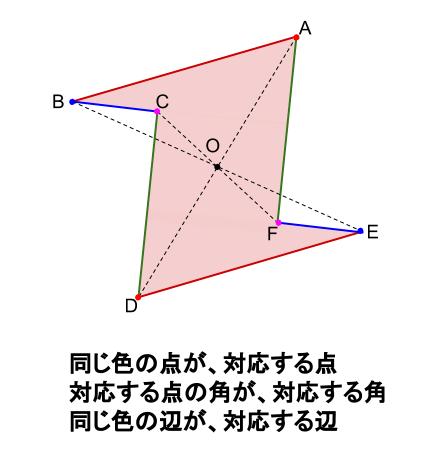
線対称のときと同様に、
対応する辺は、対応する頂点の順番にかくのがルールです。
つまり、
\(AB\) と対応する辺は \(DE\) です。
\(ED\) とかいてはいけません。
細かいことですが、ルールです。
点対称な図形の代表例
点対称な図形の代表例は平行四辺形です。
平行四辺形は点対称であり、線対称でない図形です。
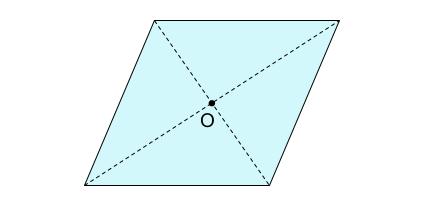
長方形、ひし形、正方形はすべて平行四辺形なので、
点対称です。
※かつ、線対称な図形でもあります。
平行四辺形以外で、
「点対称であり、線対称でない」図形は、
名前がついている有名な図形ではありません。
強いて挙げるならば、
アルファベットの \(N,S,Z\) が点対称であり、線対称でない図形の例です。
例題
点 \(O\) が対称の中心となるように、点対称な図形を完成させなさい。
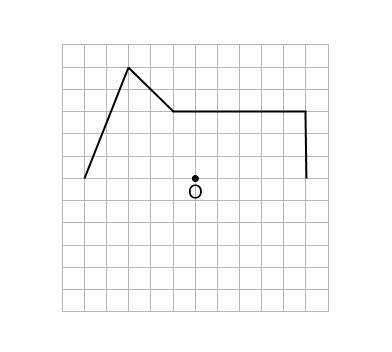
解説
作図の手順
1.対応する頂点をとる
2.点を線分で結ぶ
1.対応する頂点をとる
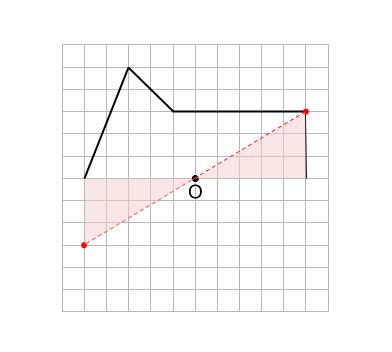
点と対称の中心を結ぶ直線をひき、距離が等しくなるように対応する点をとります。
等しい距離は、合同な直角三角形を用います。
上では、直角をはさむ \(2\) 辺の長さが \(3cm,5cm\) の直角三角形です。
※目盛りのない場合は、コンパスを用いて等しい長さを測ります。
すべての点でこれを行います。
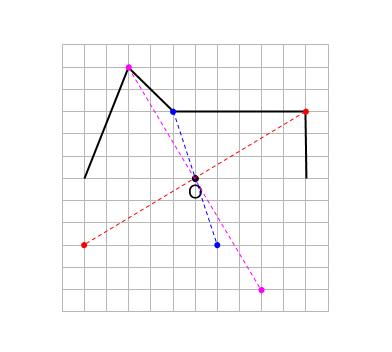
2.点を線分で結ぶ
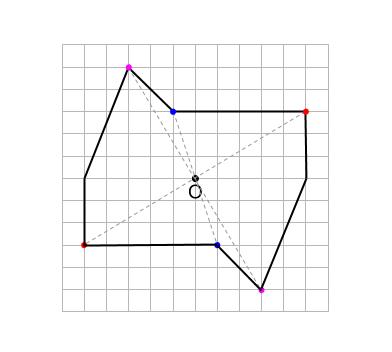
点をすべて結べば完成です。
スポンサーリンク
