線対称な図形
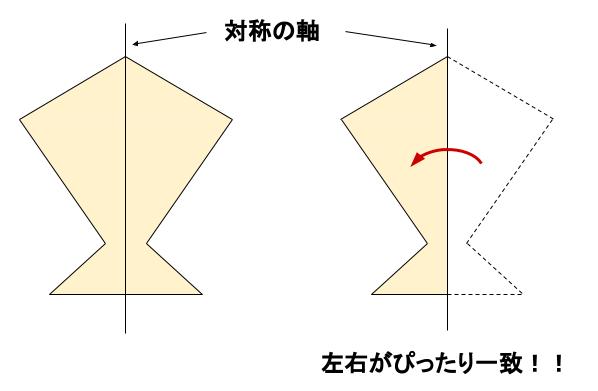
\(1\) 本の直線を折り目として折り返したとき、ぴったりと重なり合う図形を
線対称な図形といいます。
折り目となる直線を対称の軸といいます。
対応する点、角、辺
折り返してぴったりと重なる辺、点、角を、それぞれ、
対応する辺
対応する点
対応する角
といいます。
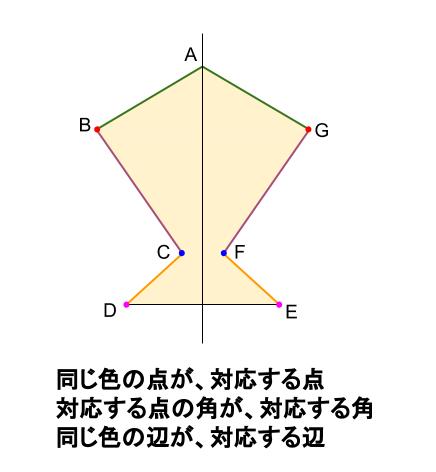
注意して欲しいこととして、
対応する辺は、対応する頂点の順番にかくのがルールです。
つまり、
\(AB\) と対応する辺は \(AG\) です。
\(GA\) とかいてはいけません。
細かいことですが、ルールです。
\(CD\) に対応する辺は \(FE\) です。
対称の軸と垂直二等分
対応する \(2\) 点を結ぶ線分は、対称の軸によって垂直に二等分されます。

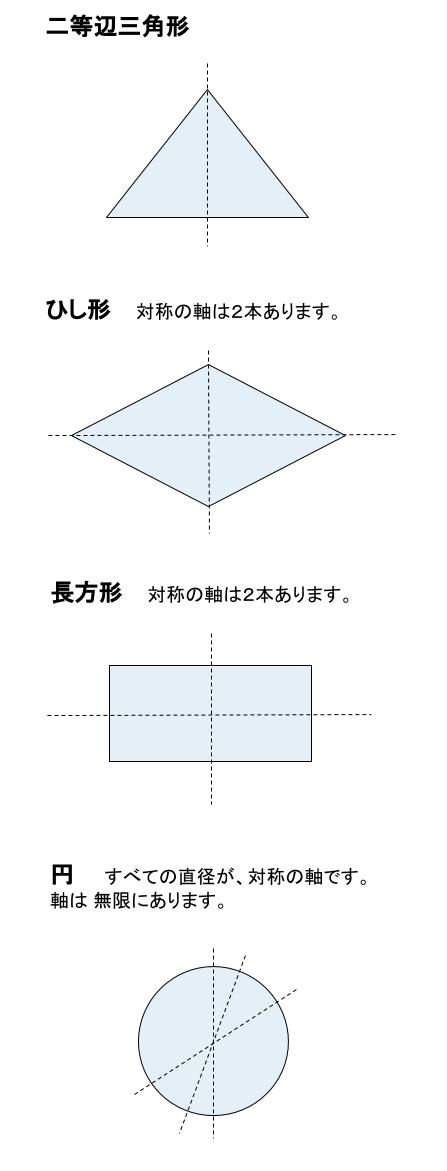
線対称な図形の代表例
線対称な図形の代表例をいくつか挙げます。
他にもいくらでもありますが、代表例です。
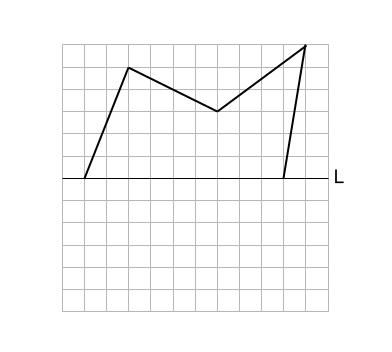
例題
直線 \(L\) が対称の軸となるように、線対称な図形を完成させなさい。
解説
作図の手順
1.対応する頂点をとる
2.点を線分で結ぶ
1.対応する頂点をとる
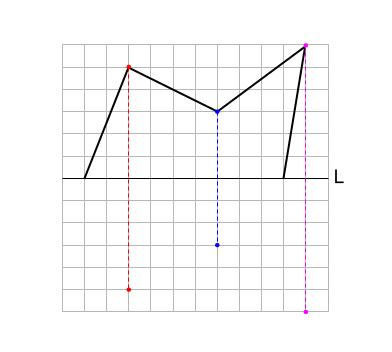
対称の軸までの距離が等しくなるように、
それぞれの対応する点をとります。
2.点を線分で結ぶ
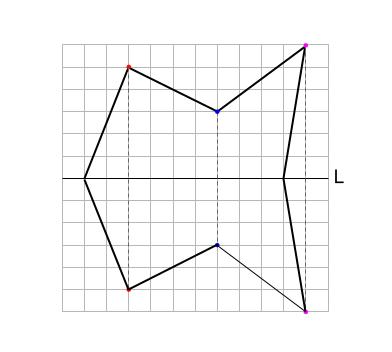
点をすべて結べば完成です。
スポンサーリンク
