折れ線の最短距離の作図
例題
直線 \(L\) 上に \(AP+BP\) の長さが最も短くなるような点 \(P\) を作図しなさい。
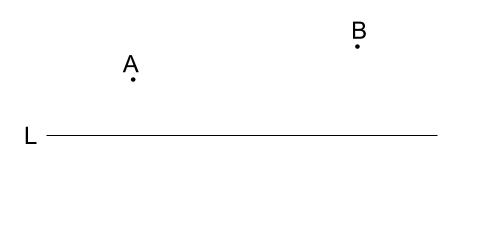
解説
点 \(P\) がどこにあるのかによって、 \(AP+BP\) の長さはさまざまに変化します。
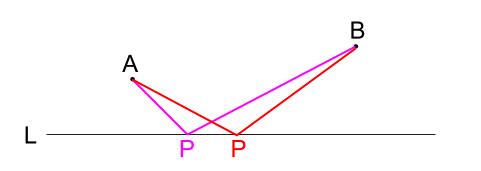
点 \(P\) をどこにすれば、 \(AP+BP\) の長さが最短になるのか。
この作図は超有名問題で、以下の解法をしっかり理解・暗記してください。
この作図を行うために必要は図形的性質の知識は、
\(L\) を対称の軸として \(A\) と対称な位置に \(A´\) をとれば、\(AP+BP=A´P+BP\)

つまり、
\(A´P+BP\) が最短となる点 \(P\) の位置が、\(AP+BP\) が最短となる位置です。
折れ線より、直線の方が短いので
\(A´P\) と \(PB\) が一直線のときが最短です。
直線 \(A´B\) と 直線 \(L\) の交点が、求める点 \(P\) の位置です。
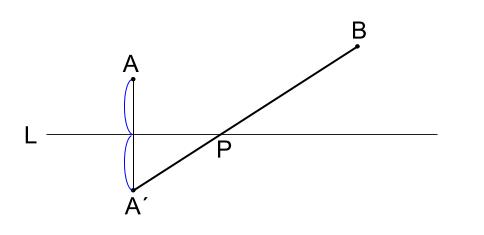
よって、作図の方針がたちました。
1.点 \(A\) と対称な点 \(A´\) を、\(L\) を対称の軸としてとる。
2.直線 \(A´B\) と 直線 \(L\) の交点を 点 \(P\) とする。
作図
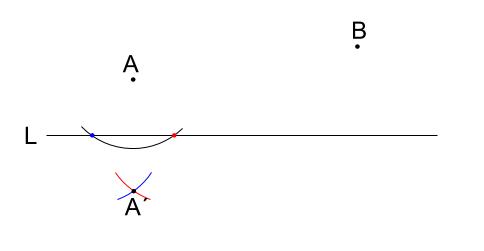
点 \(A\) を中心に円かき、直線 \(L\) との交点をとる
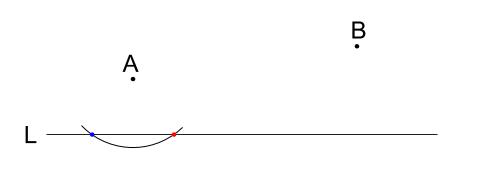
直線 \(L\) との交点を中心に円を \(2\) つかく。
この円の半径は先と同じ半径。
交点が \(A´\)
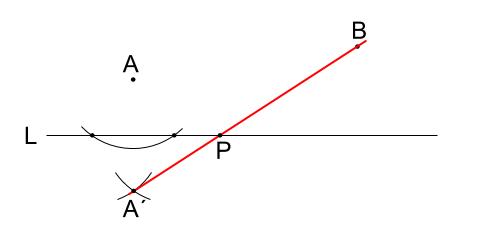
直線 \(A´B\) と直線 \(L\) の交点が \(P\)
スポンサーリンク
