中学数学の作図
作図のお約束事
中学数学で求められる作図とはある「作法」に則って進められます。
その「作法」とは、ゲームのルールのようなものです。
作図をするときの約束事
- 定規とコンパスだけを使う(もちろん鉛筆も使ってね)。
分度器は使わない。その他の道具も使わない。 - 定規は、直線(線分)をひくのに使う。長さを測ることはできない。
直線を引くとは、以下の \(2\) つのこと- 点と点を結ぶ
- あらかじめ与えられている線分を延長する
- 長さを測ることはできないが、ある \(2\) 点間の長さと同じ長さをコンパスで得ることはできる。
もちろん、長さが何\(cm\) なのかを測ることはできない。
以上 \(3\) つのルールを暗記してください。
正三角形の作図
作図の手始めに、小学校のときに既に学習している
正三角形の作図をしてみましょう。
例題1
線分 \(AB\) を \(1\) 辺とする正三角形を作図しなさい。
解答
1.コンパスで線分 \(AB\) の長さをとります。
この長さを \(r\) とします。
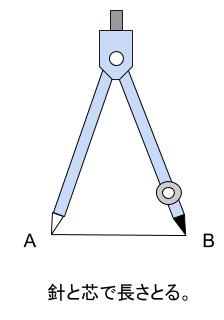
2.点 \(A\) を中心に、半径 \(r\) の円をかきます。
円は一部でOKです。
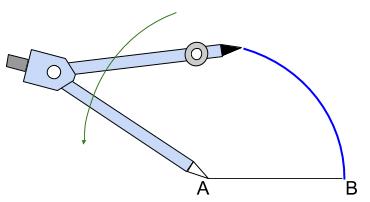
3.点 \(B\) を中心に、半径 \(r\) の円をかきます。
円は一部でOKです。
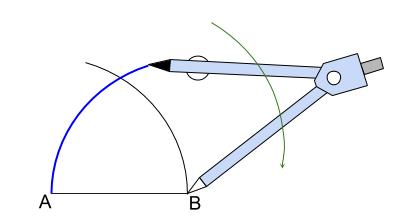
4.\(2\) つの弧の交点を \(C\) とすると、三角形 \(ABC\) は正三角形です。
\(AC\) と \(BC\) を定規で結びます。
完成です。
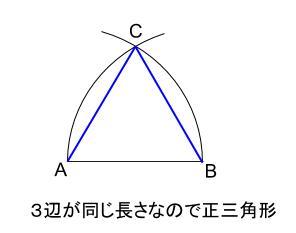
正三角形の作図手順は必ず暗記しましょう。
コンパスはこのように、同じ長さをとるために使います。
もちろん円をかくために使うこともありますが。
定規は直線をひくだけです。
ひし形の作図
ひし形の作図も小学校で学習済みです。
ひし形とは \(4\) 辺の長さが等しい四角形です。
つまり、正三角形(\(3\) 辺の長さが等しい)の作図と同じように、コンパスで同じ長さをとっていくことで作図可能です。
例題2
下の線分 \(AB\) を対角線とするひし形を作図せよ。

解答
作図すべきひし形は \(1\) 通りに定まるわけではありません。
\(1\) 辺の長さがいくつなのかによって、無数に考えられるからです。
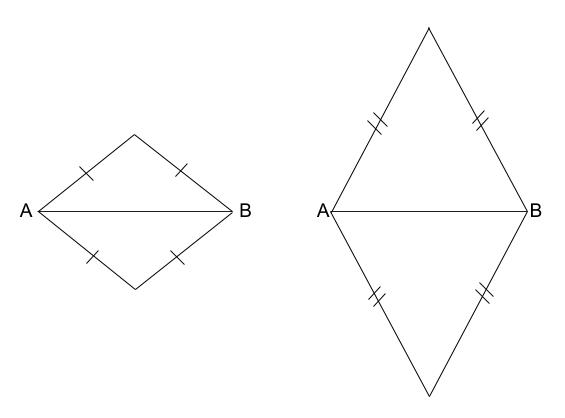
ですので、適当に \(1\) 辺の長さを決めます。
コンパスを適当な幅に広げます。
点 \(A\) を中心に円をかき、続けて同じ半径で
点 \(B\) を中心に円をかきます。
\(2\) つの弧の交点を取ることが目的です。
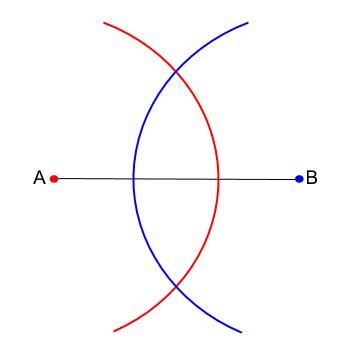
見ての通りですが、コンパスの幅は
短すぎると交わりません。
長すぎるのも何かと不便でしょう。
線分 \(AB\) の長さの \(\frac{2}{3}\) くらいがおすすめです。
下図のように交点と \(A,B\) を直線で結べば、ひし形の完成です。
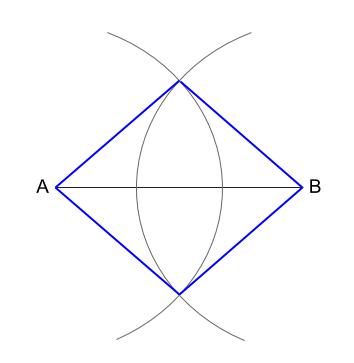
例題3
\(\angle A\) を \(1\) つの角とするひし形を作図しなさい。
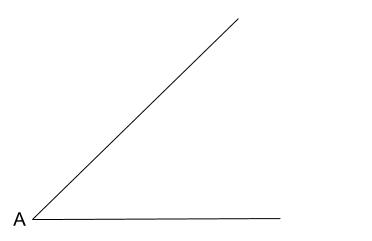
解答
先の例題同様、作図すべきひし形は \(1\) 通りに定まるわけではありません。
ひし形の \(1\) 辺の長さをいくつにするかで、無数のひし形が作図できます。
ですので、適当に \(1\) 辺の長さを決めます。
コンパスを適当な幅に広げ、\(A\) を中心に円弧をかきます。
直線との交点を \(B,C\) とします。
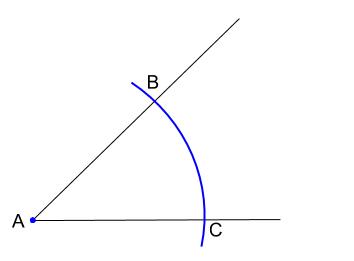
コンパスの幅を変えないで、点 \(B\) を中心に円弧をかき、続いて点 \(C\) を中心に円弧をかきます。
交点を \(D\) とします。
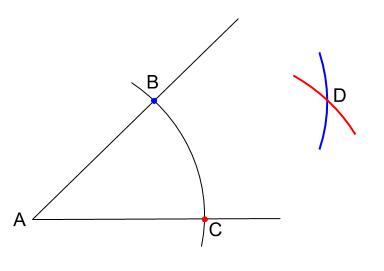
\(BD\) と \(CD\) を結ぶと、ひし形の完成です。
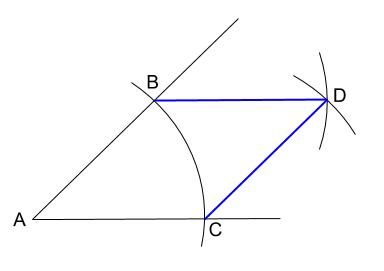
このページで扱った \(2\) 通りのひし形の作図ですが、絶対に暗記しておかないといけません。
スポンサーリンク
