また、図形特有の言葉を確認しておきましょう。
直線
直線とは正確に分類すると以下のようになります。
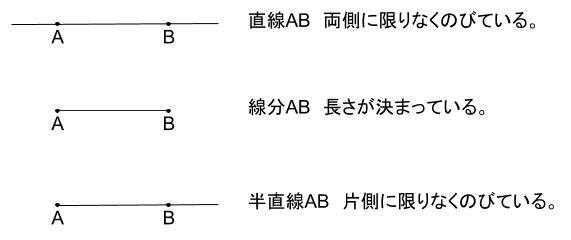
しかし、あまりこれらの言葉にこだわりすぎる必要はありません。
特に、半直線や線分という言葉はあまりでてきません。
線分は、主に図形の辺としてでてきます。
角
角の表し方は下図のように様々な表記があります。
\(\angle ABC\) は「角 \(ABC\)」と読みます。
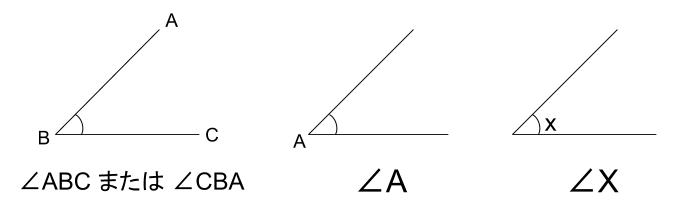
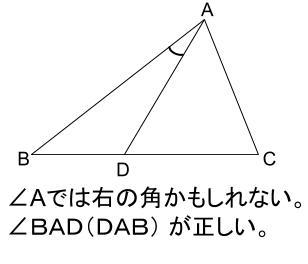
下の図の角を表したい場合は、\(\angle A\) では通じません。
\(\angle BAD\) と表記します。
三角形
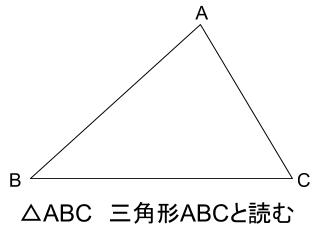
\(3\) 点 \(A,B,C\) を頂点とする三角形を \(\triangle ABC\) と表します。三角形 \(ABC\) と読みます。
平行と垂直
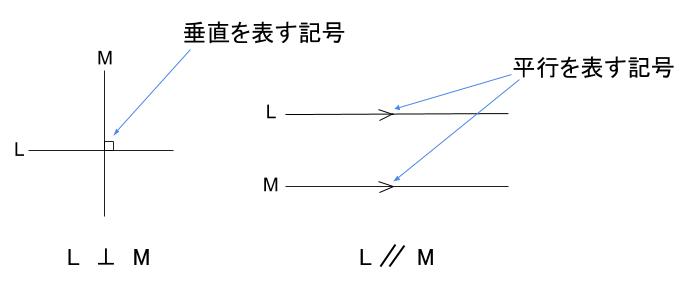
\(2\) 直線 \(L\) と \(M\) が直角に交わるとき、\(2\) 直線は垂直であるといい
\(L \perp M\) で表す。 \(L\) 垂直 \(M\) と読む
\(2\) 直線 \(L\) と \(M\) をどこまでのばしても交わらないとき、\(2\) 直線は平行であるといい
\(L /\!/ M\) で表す。(\(L\) 平行 \(M\) と読んだり、\(L\) と \(M\) は平行と読みます。)
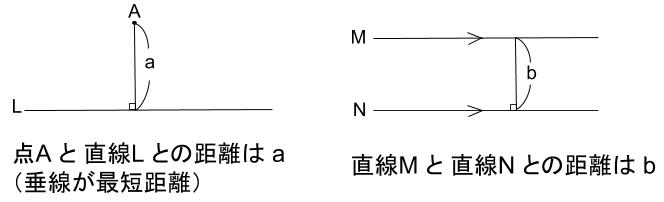
点と直線の距離
点 \(A\) と直線 \(L\) との距離とは、
点 \(A\) と直線 \(L\) との最短距離のことであり、
それは、点 \(A\) から直線 \(L\) にひいた垂線の長さである。
直線と直線の距離
直線 \(M\) と直線 \(N\) との距離は、
直線 \(M\) 上の点 \(A\) から直線 \(N\) にひいた垂線の長さである。
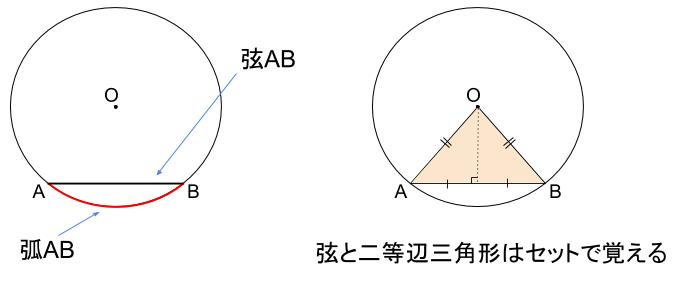
弦と弧
下図のような円 \(O\) において、
\(A\) から \(B\) までの円周の部分を弧 \(AB\) といい記号 \(\stackrel{ \Large \frown }{ AB }\)
とかく
\(AB\) を結ぶ線分を弦 \(AB\)という
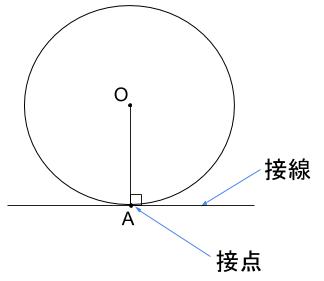
円の接線
円と直線に共通な点がただ \(1\) つのとき、円と直線は接するといい
その点を 接点、接する線を接線という
円の接線は、接点を通る直線に垂直である。
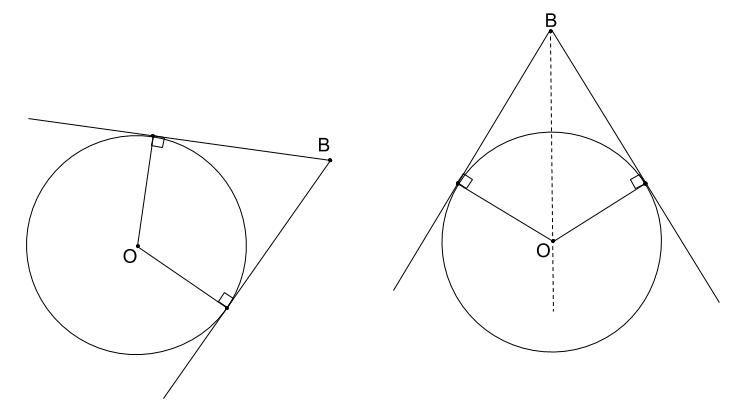
円 \(O\) の外の点 \(B\) から、円 \(O\) に接線を引くとき、必ず \(2\) 本の接線が引けます。
これが成り立つことは、点 \(B\) が真上になるように回転させて見てみれば明らかでしょう。
これは \(BO\) を結ぶ直線を中心に図形全体が左右対称となります。
\(2\) つの直角三角形が合同であることも覚えておきたいです。
スポンサーリンク
