作図の影のルール
ほとんどの作図は、
垂直二等分線
角の二等分
の \(2\) つを組合わせて行われます。
作図は最終完成形の中に、いかに「垂直二等分」や「角の二等分」を見出すかがポイントです。
※すべての作図で、とはいえませんが、ほぼすべての作図に共通です。
直線上にある点を通る垂線の作図
例題1
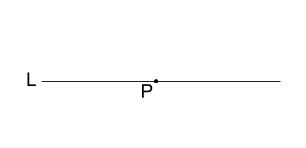
直線 \(L\) 上の点 \(P\) を通る、直線 \(L\) の垂線を作図しなさい。
解答
作図は、最終完成形から逆算して行います。
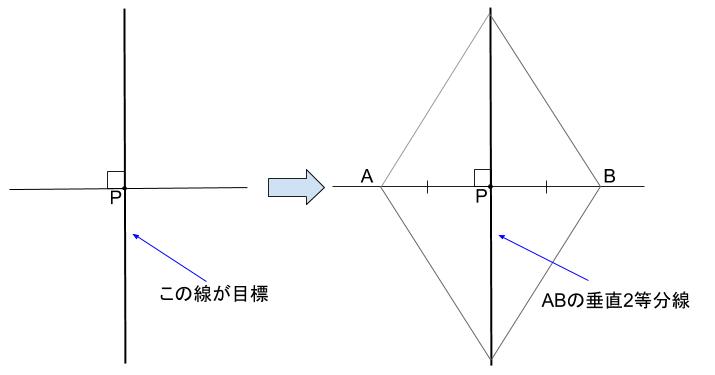
ラフスケッチは以下のようになります。
垂直二等分線の作図と似ています。
つまり、\(P\) から等距離の点 \(A,B\) があれば
垂直二等分線の作図と同じになります。
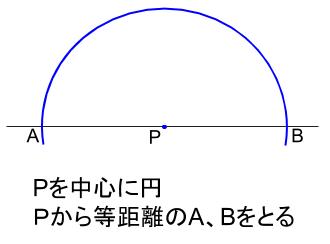
よって、
\(P\) から等距離の点 \(A,B\) をとる。
\(AB\) の垂直二等分線を作図すれば、それが求める垂線。
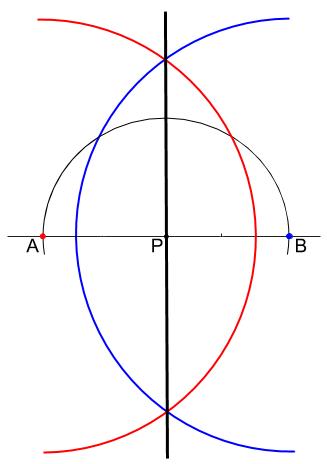
\(AB\) の垂直二等分線を作図して完成。
直線上にない点を通る垂線の作図
例題2
\(Q\) を通る、直線 \(L\) の垂線を作図しなさい。
解答
作図は、最終完成形から逆算して行います。
ラフスケッチは以下のようになります。
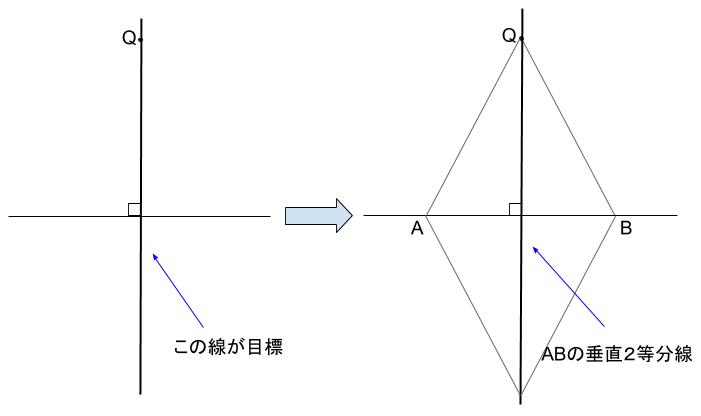
やはり垂直二等分線の作図に帰着させることができます。
\(AB\) をいかにとるか。
\(AB\) は \(Q\) から等距離にあるので、コンパスで一発ですね。
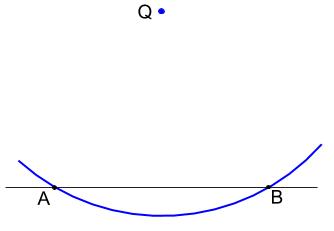
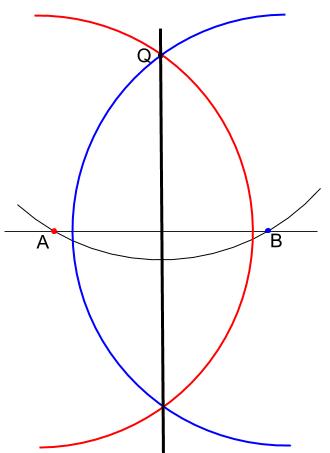
\(AB\) の垂直二等分線を作図して完成。
円弧は必ずしも点 \(Q\) を通る必要はありません。
スポンサーリンク
