【中学数学】作図・円と接線、接点

接線の作図

円 $O$ の周上の点 $A$ で、円 $O$ に接する接線を作図しなさい。

$中学数学・高校受験chu-su-　作図　円の接線　問題$

まずは完成図をラフスケッチしましょう。

接線は、中心と接点を結ぶ半径と垂直になる。
これは重要暗記事項ですよ。

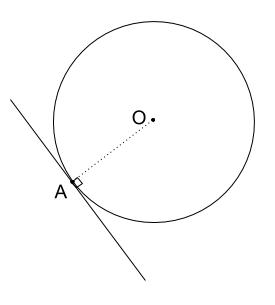
$中学数学・高校受験chu-su-　作図　円の接線　ラフスケッチ$

よって、
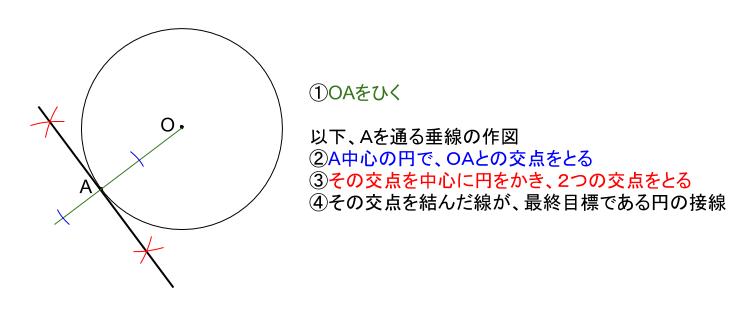
$OA$ を引き、
点 $A$ を通る、$OA$ の垂線を引けば完成とわかります。

$中学数学・高校受験chu-su-　作図　円の接線　解答図　手順$

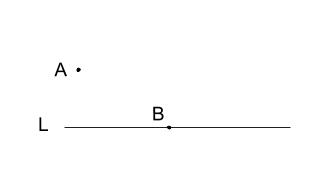
点 $B$ で直線 $L$ に接し、点 $A$ を通る円を作図しなさい。

$中学数学・高校受験chu-su-　作図　接線と円　問題$

まずは完成図をラフスケッチしましょう。

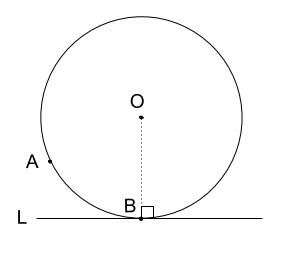
$中学数学・高校受験chu-su-　作図　接線と円　ラフスケッチ１$

円をかくということは、円の中心 $O$ を定めるということです。
上の図をみて、中心 $O$ をいかに見つけ出すのかを考えてみてください。
点 $A,B$ と直線 $L$ と、中心 $O$ がいかなる関係で繋がっているのか。

中心 $O$ は
$L$ の垂線上にある（点 $B$ を通る垂線）。
$OA$ と $OB$ は円 $O$ の半径なので、等しい長さ　⇒ $A,B$ から等距離にある＝ $AB$ の垂直二等分線上にある

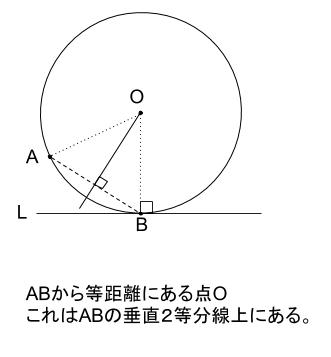
$中学数学・高校受験chu-su-　作図　接線と円　ラフスケッチ２$

よって、
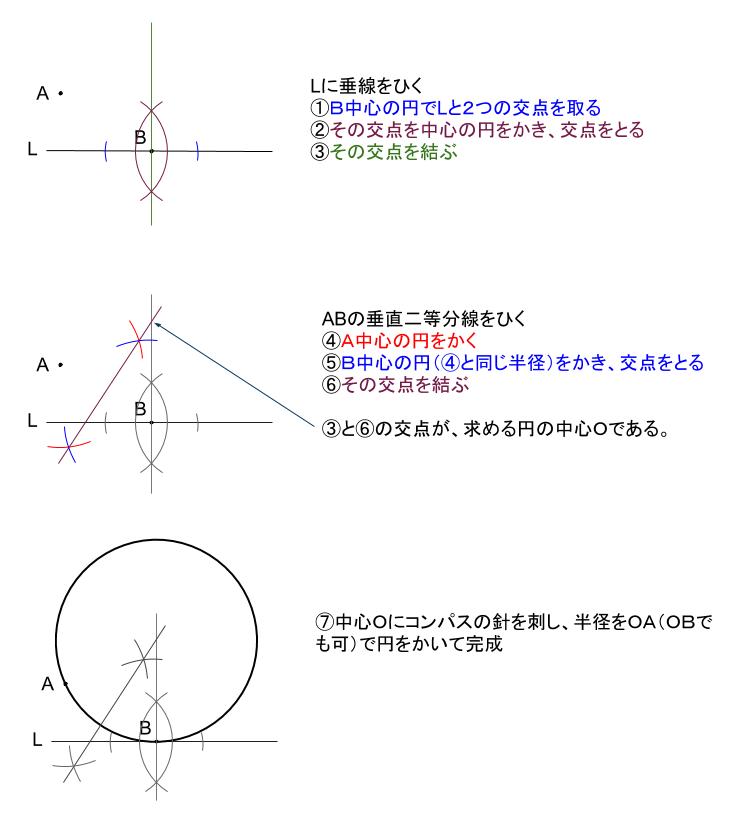
$B$ を通る、$L$ の垂線を作図。
$AB$ の垂直二等分線を作図。
この $2$ 本の直線の交点が $O$
$O$ を中心に、コンパスで半径が$OB（OA）$となるように円をかいて完成。

$中学数学・高校受験chu-su-　作図　接点に円の作図　解答図　手順$