正負の数・正の数を足す、引く

正の数を足す、引く

小学校までは、正の数しか出てきませんでした。
例えば以下のような計算です。

• 正　＋　正

\(5+7=12\)

• 正　－　正

\(9-2=7\)

さらに引き算に制限がありました。

\(4-7=\)

このようなときは「引けない」でしたね。
ですから、そもそもこのような計算は目の前に現れませんでした。

しかし、負の数まで考えれば、この引き算も可能です。
今後はどんどん出てきます。

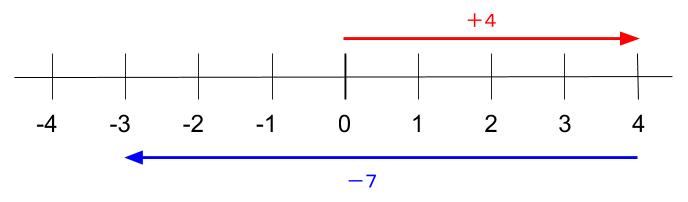
数直線で正方向（右）、負方向（左）に移動を考えます。
\(4-7=-3\)
です。

０よりも小さい負の数の世界まで数直線を伸ばしたので、
引き算に制限がなくなりました。
どんな数でも引くことができるようになったのです。
４円しかないのに７円使ったらどうなるのか。
３円の借金になる。
これは感覚的にあたりまえである、というレベルまで練習しましょう。

様々な参考書、サイトで紹介されている

「符号が違うときは、数字の大きいほうの符号をつけて、数字は引き算」

のように言葉で身につけることではありません。
直感的に「あたりまえ」と思えるようになることが大事です。
呪文のようにルールを唱えて、わけのわからない操作で答えを出すことは絶対にやめましょう。
数直線で、右に、左に進むイメージを持つだけです。
数学の得意な人ならば、必ずもっているイメージです。

混乱のもと？？符号なのか演算記号なのか？

上で見た計算
\(4-7=-3\)
なんですけど・・・どのように読みますか？

よん　引く　なな　イコール　マイナスさん　
と読めば上で教えた通りですけど

よん　マイナスなな　イコール　マイナスさん
のように読む指導も学校などで普通に行われています。

この読み方をすると、－７（マイナスなな）の箇所が

• 正の数である７を引いているのか
• 負の数である－７が４にくっついているのか

どっち？？
という混乱が生じます。
こんな混乱起きたことない、困ったことはないという方はそれでOKなんですけど、
初学者がこのあたりで混乱することは普通のことです。

この混乱の最大の原因は
「符号を表す記号の＋、－」と「演算の記号の＋、－」
異なる意味のものに、同じ記号が使われているからです。

符号の－なのか、演算の－なのかを区別するために、
「読み方を変える」ことを強くおススメします。

記号を自分勝手に変えることはできませんので、
読みかたを変えて区別しましょう。

中学生からはじまった正負の符号

符号を表す＋はプラス
符号を表す－はマイナス
と読む。

小学生のときからやっていた足し算、引き算の記号

今まで通り、
演算の＋は足す
演算の－は引く
と読む。

符号なのか演算なのかの見分け方ですが、
数のすぐ後ろにある記号は演算の記号です！！

例

• \(5+7=\)　ご　足す　なな　は
• \(9-2=\)　きゅう　引く　に　は
• \(4-7=\)　よん　　引く　　なな　は
• \(-3-2=\)　マイナスさん　引く　に　は

　正の数であることを強調するための表記

上で考えた、\(4-7=-3\)　ですが、
これが
正の数　\(4\)
から
正の数　\(7\)
を引いている
ということを強調するために以下のような表記をすることもあります。

\((+4)-(+7)=-3\)
あるいは
\(4-(+7)=-3\)

これらは、当然、
\(4-7=-3\)

と同じ式です。
小学校のときに、正の数３をいちいち（＋３）とは表記しませんでしたね。
ですので、（　）に囲われた正の数がでてきたら、（　）や＋を取り除いてしまいましょう。
ただ取り除くだけでＯＫです。

次に、負の数に正の数を加減してみましょう

負の数＋正の数

負の数に正の数を足します。

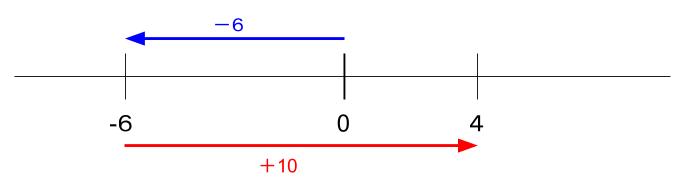
\(-6+10\)

マイナスろく　足す　じゅう　と読みましょう。

６円借金していたところに、１０円の収入があった。
借金を返して、自分の手元には４円残りますね。

\(-6+10=4\)

次に
\(-5+3\)

これも大丈夫ですね。

\(-5+3=-2\)
です。
借金を３円返してもなお、あと２円の借金があります。

負の数－正の数

次に負の数から正の数を引きます。

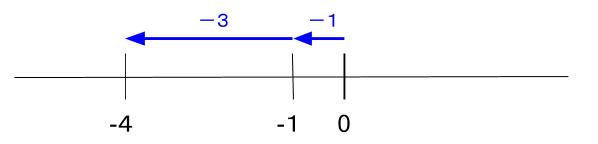
\(-1-3\)

マイナスいち　引く　さん　　　と読みましょう。

\(-1-3=-4\)
１円の借金があるとき、さらに３円失ったら・・・
４円の借金、－４　となります。

これも感覚的に迷わず計算できますね！

例題１

次の計算をしなさい。
① \(5-8\)
② \(-2-(+6)\)
③ \(1-5-2+3\)

解答

① \(-3\)
数直線で、右に左に移動するイメージが大事です。

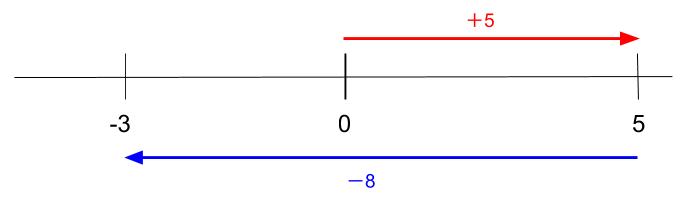
\(5-8=-3\)
です。

② \(-8\)
\(+6\) → \(6\) です。
正の数は、小学校のときに使用していた表記、(　)　も　＋　もない表記に
しましょう。
つまり、
\(-2-(+6)=-2-6\)
を計算します。

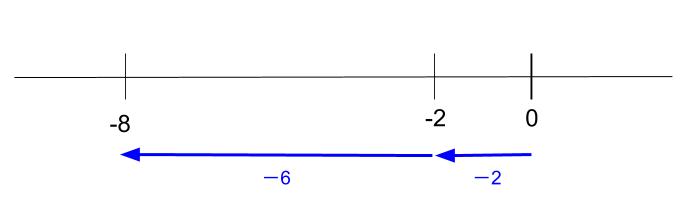
\(-2-(+6)=-2-6=-8\)
です。

③ \(-3\)
右移動チームと、左移動チームをまとめましょう。
\(1-5-2+3=1+3-2-5\)
ということです。
※加減だけの式において、計算順序を入れかえてよいことを
交換法則が成り立っているといいます。
あまり深入りしなくて良い話題です。

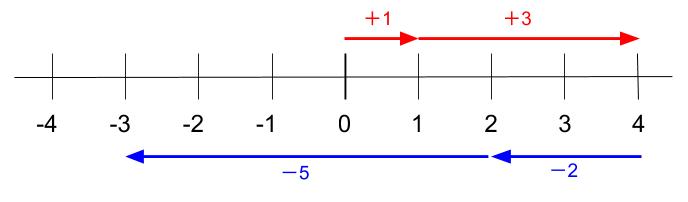
\(1-5-2+3=1+3-2-5\)
\(=4-7\)
\(=-3\)
です。

練習問題

次の計算をしなさい。
① \(3-7\)
② \(-1-(+8)\)
③ \(-5-2+9\)
④ \(6-3+2-5\)

解答

① \(-4\)
② \(-9\)
③ \(2\)
④ \(0\)