代表値
資料の特徴を表す値を代表値といいます。
平均値、最頻値、中央値
などがあります。
このページでは、「中央値」について学習しましょう。
中央値
資料の値を大きい順に並べたとき、中央の値を中央値(メジアン)といいます。
奇数個の中央値
例
\(9\) 人の生徒の通学時間(分)
\(6, 13 , 15 , 10 , 12 , 24 , 15 , 8 , 18 \)
この \(9\) 人の通学時間の中央値を求めてみましょう。
\(9\) 個の資料を大きい順に並べると、
\(24 , 18 , 15, 15, 13 , 12 , 10 , 8 , 6\)
であり、ちょうど真ん中の値は \(13\) です。
\(13\) より大きい資料が \(4\) つ、
\(13\) より小さい資料が \(4\) つ、
\(13\) がちょうど真ん中ですね。
よって、求める中央値は \(13\)(分)です。
偶数個の中央値
資料の個数が偶数個の場合、ちょうと真ん中になる資料はありません。
真ん中 \(2\) つの平均を中央値とします。
例
\(8\) 人の生徒の身長 \((cm)\)
\( 156 , 152 , 148 , 164 , 159 , 168 , 160 , 155\)
この \(8\) 人の身長の中央値を求めてみましょう。
\(8\) 個の資料を大きい順に並べると、
\(168 , 164 , 160 , 159 , 156 , 155 , 152 ,148 \)
であり、真ん中の値は \(159\) と \(156\) です。
この \(2\) つの平均が、偶数個の資料の中央値です。
\((159+156)÷2=157.5\)
よって、求める中央値は \(157.5(cm)\) です。
度数分布表からの中央値
度数分布表からは、各資料の真の値はわかりません。
よって、階級値を用います。
例1
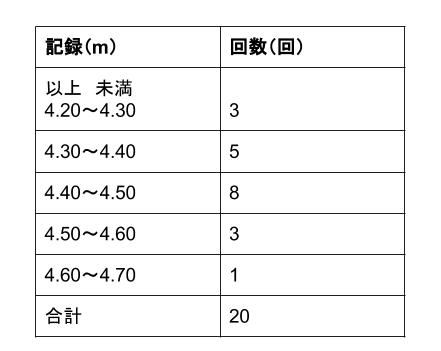
表は、\(A\) さんの走り幅跳び \(20\) 回の記録である。
中央値を求めなさい。
解説
\(20\) 個の資料の中央値なので、
\(10\) 番目と \(11\) 番目の値の平均をとります。
\(10\) 番目の値は、\(4.40~4.50\) の階級の中にあるので、階級値 \(4.45\) です。
\(11\) 番目の値も、\(4.40~4.50\) の階級の中にあるので、階級値 \(4.45\) です。
この \(2\) つの値の平均が求める中央値で、もちろん
\(4.45\)
となります。
例2
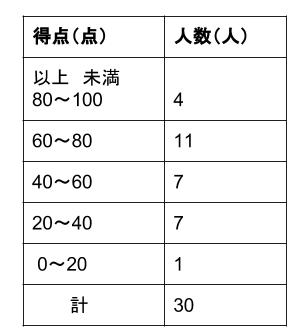
表は、あるクラス \(30\) 人の英語のテストの記録である。
中央値を求めなさい。
解説
\(30\) 個の資料の中央値なので、
\(15\) 番目と \(16\) 番目の値の平均をとります。
\(15\) 番目の値は、\(60~80\) の階級の中にあるので、階級値 \(70\) です。
\(16\) 番目の値は、\(40~60\) の階級の中にあるので、階級値 \(50\) です。
この \(2\) つの値の平均が求める中央値です。
\((70+50)÷2=60\)
となります。
スポンサーリンク
