反比例とは
\(2\) つの量 \(x\) と \(y\) の関係が、
\(y=\displaystyle \frac{a}{x}\) \((aは0でない値)\)
という式で表されるとき、
\(y\) は \(x\) に反比例するといいます。
このときの \(a\) を比例定数といいます。
※正比例のときと同じ、「比例定数」です。
反比例の具体例・速さ
反比例する \(2\) つの量とはどのようなものか。
具体例で見てみましょう。
\(600m\) の道のりを分速 \(xm\) で進んだときにかかった時間を \(y\) 分とするとき、
\(y\) を \(x\) の式で表すと
\(時間=距離÷速さ\) なので
\(y=\displaystyle \frac{600}{x}\)
となり、\(y\) と \(x\) は反比例します。
反対に比例する・反比例
反比例の大雑把なイメージですが、
\(x\) の値が大きくなると
反対に
\(y\) の値が小さくなる
このような \(2\) 量の関係です。
※反対の比例で反比例です。
今回の例では、
\(x\) が大きくなるとは、「速く進む」ということです。
すると
短い時間で着くので、 \(y\) が小さくなります。
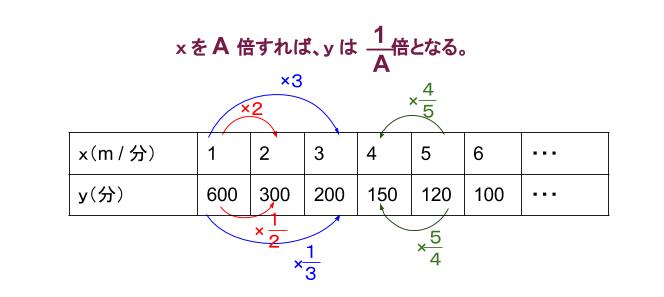
上の表で確認できるように、
反比例では \(x\) が \(2\) 倍、\(3\) 倍、\(4\) 倍・・・になると、
\(y\) は \(\displaystyle \frac{1}{2}\) 倍、 \(\displaystyle \frac{1}{3}\) 倍、 \(\displaystyle \frac{1}{4}\) 倍・・・になります。
反比例は積一定の関係
反比例の式は、
\(y=\displaystyle \frac{a}{x}\)
ですが、式変形をすると
\(xy=a\) \((aは0でない値)\)
となります。
つまり、\(x\) と \(y\) の積が一定となる関係です。
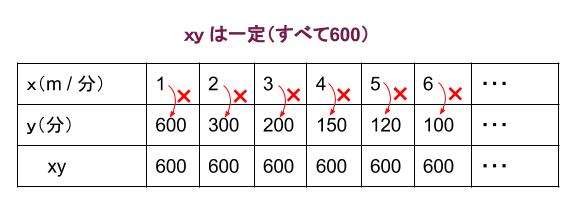
ですから、
\(速さ×時間=距離\)
において、距離が一定のときの
速さと時間の関係は反比例します。
上の例で見た通りです。
他にも
長方形の面積は
\(よこの長さ×たての長さ=面積\)
ですから、面積が一定のときの
よこの長さとたての長さの関係は反比例します。
例題1
次の数量関係において、\(y\) を \(x\) の式で表し、その関係が比例なら〇
反比例なら△、どちらでもないものには×をつけなさい。
① 毎分 \(80m\) で \(x\) 分間歩いたときの距離 \(ym\)
② 周の長さが \(36cm\) である長方形の、たての長さ \(xcm\) とよこの長さ \(ycm\)
③ 底辺 \(xcm\)、高さ \(ycm\) の三角形の面積が \(20cm^2\)
④ 長さ \(3m\) のひもから、 \(xm\) 切り取ったときの残り \(ym\)
解説
①毎分 \(80m\) で \(x\) 分間歩いたときの距離 \(ym\)
\(y=80x\)
となるのでこれは比例、よって○
②周の長さが \(36cm\) である長方形の、たての長さ \(xcm\) とよこの長さ \(ycm\)
たてとよこの長さを足せば、長方形の周の半分なので、
\(y+x=36×\displaystyle \frac{1}{2}\)
これを\(y=\) の形に整理すると
\(y=18-x\)
これは、比例でも反比例でもないので、×
③底辺 \(xcm\)、高さ \(ycm\) の三角形の面積が \(20cm^2\)
三角形の面積の公式通りなので、
\(\displaystyle \frac{1}{2}xy=20\)
よって
\(y=\displaystyle \frac{40}{x}\)
これは反比例なので、△
④長さ \(3m\) のひもから、 \(xm\) 切り取ったときの残り \(ym\)
\(y=3-x\)
となるので、比例、反比例、どちらでもない。
よって、×
例題2
\(y\) が \(x\) に反比例し、対応する \(x,y\) の値が次のとき、 \(y\) を \(x\) の式で表しなさい。
① \(x=6\) のとき \(y=3\)
② \(x=3\) のとき \(y=-3\)
解説
「\(y\) が \(x\) に反比例」とあれば、何も考えずに
\(y=\displaystyle \frac{a}{x}\)
とします。
この式の比例定数、\(a\) を求めればよいのです。
①\(x=6\) のとき \(y=3\)
「\(y\) が \(x\) に反比例」とあるので、
\(y=\displaystyle \frac{a}{x}\)
これに、\(x=6\) と \(y=3\) を代入します。
\(3=\displaystyle \frac{a}{6}\)
なので、
\(a=18\)
これは、\(y=\displaystyle \frac{a}{x}\) の \(a\) が求まったので、
\(y=\displaystyle \frac{18}{x}\)
これが求める式となります。
②\(x=3\) のとき \(y=-3\)
「\(y\) が \(x\) に反比例」とあるので、
\(y=\displaystyle \frac{a}{x}\)
これに、\(x=3\) と \(y=-3\) を代入します。
\(-3=\displaystyle \frac{a}{3}\)
なので、
\(a=-9\)
これは、\(y=\displaystyle \frac{a}{x}\) の \(a\) が求まったので、
\(y=\displaystyle \frac{-9}{x}\)
つまり、
\(y=-\displaystyle \frac{9}{x}\)
これが求める式となります。
比例定数が負の数というのもアリなのです!
スポンサーリンク
