分配法則
分配法則とは、下のような( )をはずす計算ルールのことです。
\(a(b+c)=ab+ac\)
\(a(b-c)=ab-ac\)
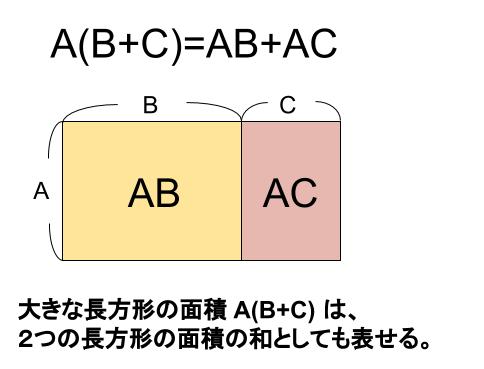
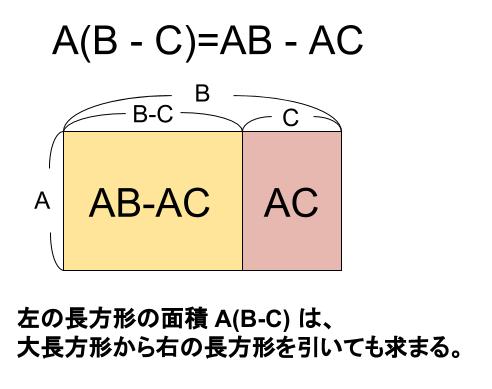
※\(a,b,c\) が負の数であったり、\(b,c\) の大小関係次第でこの図は万能ではありません。イメージがついてもらえればOKです。
要は、スラスラ計算できるようになることが重要です。
具体例で分配法則をマスターする
符号の組合せのあらゆるパターンを見ていきましょう。
例1
\(2(a+3)=2a+6\)
すべて正の符号のこのパターンは迷わないですね!
例2
\(2(a-3)=2a-6\)
これも直感と一致する計算結果でしょう。
細かく計算ルールを考える必要はないと思いますが・・・
例3
\(-2(a+3) = -2a-6\)
迷わずこの符号がわかれば、それでOKです。
しかし、符号がどのようなルールで決まるのか
迷ってしまう人もでてくる頃ですね。
計算をどのようにするのか(符号の決めかた)について、\(2\) 通りのやり方を紹介します。
\(2\) つのかけ算の結果をただ並べる方式

この方式を最もオススメします。
機械的に、何も考えずに計算ができます。
もちろんあらゆる符号のときに適用できます。
上の例1、例2も当然これを適用することで正しく計算できます。
分配法則の公式に忠実に従う

とても丁寧な途中過程ですが、
毎回これをやるのは面倒です。
圧倒的に、「ただ並べる方式」をおススメします。
例4
\(-2(a-3)=-2a+6\)
これも、「ただ並べる方式」をおススメしますが、もう\(1\) つのやり方も紹介しておきます。
\(2\) つのかけ算の結果をただ並べる方式

あまり意味を考えずに、機械的に処理をしてしまうのがおススメです。
分配法則の公式に忠実に従う

とても丁寧な途中過程ですが、
毎回これをやるのは面倒です。
圧倒的に、「ただ並べる方式」をおススメします。
マイナスは逆向きにする
次の式の( )をはずしなさい。
① \(-(a+2)\)
② \(-(a-2)\)
解説
① \(-(a+2)=-1×(a+2)\)
ということですから、分配法則で計算すれば良いですね。
もちろん、ただ並べる方式がおススメです。
\(-(a+2)\)
\(=-1×(a+2)\)
\(=-a-2\)
しかし、負の符号は、逆向き!という理解で問題ありません。
( )にマイナスが付いていれば、( )の中の符号を逆にする、
という理解でOKです。

② \(-(a-2)=-a+2\)
負の符号は、逆向き!でOKです。

分配を分けて行うことも可能
おまけ程度に。一応知っておくと便利かもしれません。
次の式の、( )をはずしなさい。
① \(-3(2a+5)\)
② \(-3(2a-5)\)
解説
もちろん、上で説明した通りに計算すればそれでOKです。
別解として、以下のような途中式を紹介します。
負の符号の扱いがどうしても苦手な人は、いろいろな方法を試してみてください。
①
\(-3(2a+5)\)
\(=-1×3×(2a+5)\) ・・・\(-3\) を \(-1×3\) としました。
\(=-1×\underline{3×(2a+5)}\)
\(=-1×\underline{(6a+15)}\)・・・下線部分を先に計算
\(=-6a-15\) ・・・マイナスは符号を入れかえ!
②
\(-3(2a-5)\)
\(=-1×3×(2a-5)\) ・・・\(-3\) を \(-1×3\) としました。
\(=-1×\underline{3×(2a-5)}\)
\(=-1×\underline{(6a-15)}\)・・・下線部分を先に計算
\(=-6a+15\) ・・・マイナスは符号を入れかえ!
例題
次の式の( )をはずしなさい。
① \(\displaystyle \frac{1}{2}(4x-3)\)
② \(-(8a-3)÷(-4)\)
③ \(\displaystyle \frac{2(3a-2)}{3}×9\)
解説
積をただ並べる方式がおすすめです。
① \(\displaystyle \frac{1}{2}(4x-3)\)
\(=\underline{\displaystyle \frac{1}{2}×4x}\) \(\underline{\displaystyle \frac{1}{2}×(-3)}\)
\(=\underline{2x}\) \(\underline{-\displaystyle \frac{3}{2}}\)
\(=2x-\displaystyle \frac{3}{2}\)
② \(-(8a-3)÷(-4)\)
まず符号を決めます。負÷負=正です。
\(=(8a-3)÷4\)
\(=(8a-3)×\displaystyle \frac{1}{4}\)
\(=\underline{8a×\displaystyle \frac{1}{4}}\) \(\underline{-3×\displaystyle \frac{1}{4}}\)
\(=\underline{2a}\) \(\underline{-\displaystyle \frac{3}{4}}\)
\(=2a-\displaystyle \frac{3}{4}\)
③ \(\displaystyle \frac{2(3a-2)}{3}×9\) ・・・約分からです。
\(=2(3a-2)×3\)
\(=6(3a-2)\)
\(=18a-12\)
スポンサーリンク
