負の数の導入・数直線

正負の数

今まで、小学校で使ってきた数はすべて０より大きい数でした。
この、「０より大きい数」のことを「正の数」といいます。
そして、「０より小さい数」のことを「負の数」といいます。

日常で負の数に触れる代表例は、「温度」です。
0℃より寒い（冷たい）ときに、－３℃のような表現をすることを知っていますね。
負の数は、数字のまえに－（マイナス）をつけて表します。
※マイナス３℃と読みます
正の数は、＋（プラス）をつけて表すこともありますが、省略することがほとんどです。

温度計の目盛りは、数直線と同様のものです。
今後、正負の数の理解のためには、数直線という視覚的イメージを大事にしていきましょう。

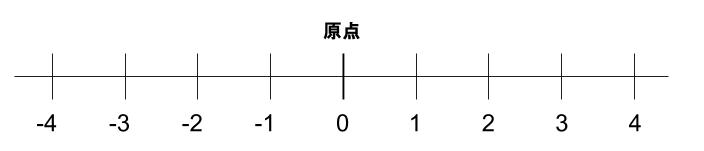
負の数とは、０より小さい方向に進んでいく数であるといえます。
正の数とは逆の向きなのですね。

数直線で、0の点を原点といいます。原点より右側が正の数、左側が負の数です。
０は正負、どちらの数でもありません。
右に行くほど大きい数で、左に行くほど小さい数です。

０より大きい整数のことを自然数といいます。

絶対値

数直線上で、原点からの距離を絶対値といいます。

３の絶対値は３
－３の絶対値も３です。

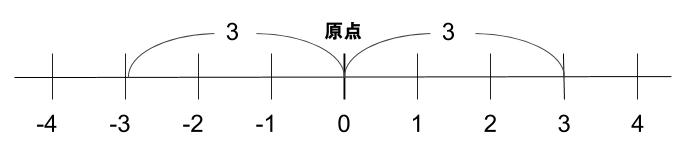
０の絶対値は０です。

不等号

数の大小は不等号（ ＜ 、＞ ）を使って表します。
数直線で、右に行くほど大きい数、左に行くほど小さい数です。

－2より1のほうが大きいことを不等号で表すと　　－2＜１　または　 １＞ －2　となります。
大きい数の方に、広がっている側を向けます。

例題１

次の数について、下の問いに答えなさい。
\(-1.2, +7, -5, 0, \displaystyle \frac{2}{3}\)

①整数をすべて答えなさい
②正の数をすべて答えなさい。
③負の数をすべて答えなさい。
④自然数をすべて答えなさい。

解答

①\(+7,-5,0\)
②\(+7,\displaystyle \frac{2}{3}\)・・・符号のない \(\displaystyle \frac{2}{3}\) も正の数です。
③\(-1.2,-5\)
④\(+7\) ・・・自然数とは正の整数のことです。\(0\) は自然数でないと覚えましょう。

例題２

次の問いに答えなさい。
①\(3\) 年前を \(-3\) 年と表すとき、\(4\) 年後はどのように表されますか。

②ある地点から \(2km\) 北の地点を \(+2km\) と表すとき、 \(5km\) 南の地点は、どのように表されますか。

解答

① \(+4\) 年

時間の流れを数直線に見立てています。
過去を負の方向と見れば、
未来は正の方向です。
現在が \(0\) 、原点ですね。

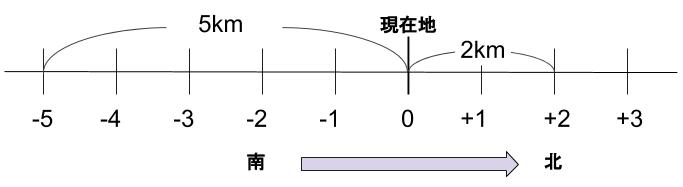
② \(-5km\)
南北の方向を数直線に見立てています。
北を正の方向と見れば、
南は負の方向です。
今いる地点が \(0\) 、原点ですね。
※北を上にするのが見慣れた向きですが、下図のように左右にしても
何の問題もありませんね。

例題３

次の問いに答えなさい、
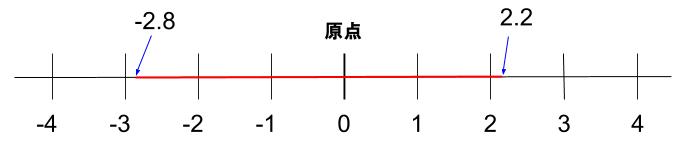
①数直線上で、\(-2.8\) と \(+2.2\) の間にある整数をすべて答えなさい。
②\(-1.7\) よりも大きい整数の中で、最も小さい整数を答えなさい。

解答

①\(-2,-1,0,1,2\)
下の数直線の赤い範囲にある整数が答えです。

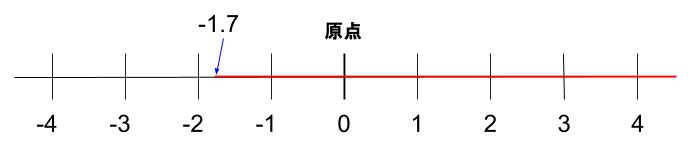
②\(-1\)
下の数直線の赤い範囲が、\(-1.7\) よりも大きい数の範囲なので、
このなかで最小の整数は \(-1\) となります。

例題４

次の問いに答えなさい。
①絶対値が \(3.5\) 以下の整数をすべて答えなさい。
②\(-0.75,-\displaystyle \frac{7}{12},-\displaystyle \frac{2}{3}\) の大小を、不等号を使って表しなさい。

解答

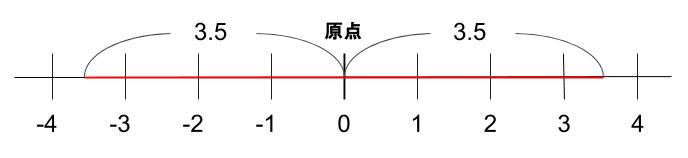
① \(-3,-2,-1,0,1,2,3\)
絶対値とは、原点からの距離のことです。
よって、絶対値が \(3.5\) 以下の数の範囲は、下図の赤い部分です。
この部分にある整数が答えです。

②　\(-0.75 \lt -\displaystyle \frac{2}{3} \lt -\displaystyle \frac{7}{12}\)
絶対値の大小比較をします。
負の数は、原点から遠く離れるほど小さいので
（原点から左に行くほど小さい）
絶対値が大きい数ほど小さくなります。

通分すると、
\(-0.75=-\displaystyle \frac{9}{12}\)

\(-\displaystyle \frac{2}{3}=-\displaystyle \frac{8}{12}\)
つまり大小関係は、
\(-\displaystyle \frac{9}{12} \lt -\displaystyle \frac{8}{12} \lt -\displaystyle \frac{7}{12}\)

よって、
\(-0.75 \lt -\displaystyle \frac{2}{3} \lt -\displaystyle \frac{7}{12}\)