式の値

代入と式の値

文字式の文字に、数を入れることを代入といいます。
代入した結果得られた値を、式の値といいます。
代入とは、代わりに入れることです。等しい量の何かに代えることです。
※厳密には、文字に「式」を入れることもあります。

さっそく例を見てましょう。

例題１

次の式の値を求めなさい。
\(x=3\) のときの、\(4x+10\) の値

解答

\(x\) に \(3\) を代入します。
\(4×(3)+10=22\)
代入する数値は、（　）をつけましょう。

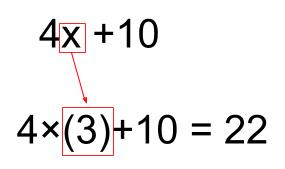
※正の数を代入するとき、（　）をつけなくとも構いませんが、正はつけない、負はつける、と覚えるよりも、
代入は（　）をつけて行う、と統一した方がミスが減ります。

例題２　負の数の代入

次の式の値を求めなさい。
\(a=-2\) のときの、\(4a^3-5\) の値

解答

負の数を代入するときは、必ず（　）をつけてから代入します。
符号ミスをしないためです。

\(4×(-2)^3-5\)
\(=4×(-8)-5\)
\(=-32-5\)
\(=-37\)

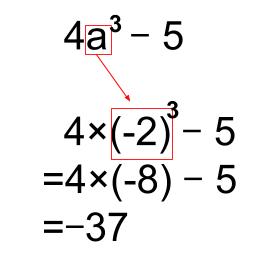
例題３　分数に代入

次の式の値を求めなさい。
\(x=\displaystyle \frac{2}{3}\) のときの、\(\displaystyle \frac{4}{x}\) の値

解答

分数式に代入するときは、÷を使った表記になおしてから代入するとよい。

\(\displaystyle \frac{4}{x}\)
\(=4÷x\)
\(=4÷(\displaystyle \frac{2}{3})\)
\(=4×(\displaystyle \frac{3}{2})\)
\(=6\)

例題4

次の式の値を求めなさい。
\(x=\displaystyle \frac{2}{3}\) のときの、\(-2(x+2)+5(x-1)\) の値

解答

いきなり代入して計算することも可能ですが、
まずは \(1\) 次式を計算してまとめましょう。
それから代入した方が楽です。

\(-2(x+2)+5(x-1)\)
\(=-2x-4+5x-5\)
\(=3x-9\)
これに、\(x=\displaystyle \frac{2}{3}\) を代入します。

\(3x-9\)
\(=3×(\displaystyle \frac{2}{3})-9\)
\(=2-9\)
\(=-7\)

スポンサーリンク