例題1
\(2\) けたの整数と、その数の十の位の数と一の位の数を入れかえた数との差は、\(9\) の倍数になることを文字を使って説明しなさい。
解説
まず問題の意味をしっかりと理解しておきましょう。
その数の十の位の数と一の位の数を入れかえた数
とありますが、この意味がわかりますか?
具体例で確認しておきましょう。
例えば、\(2\) けたの整数を \(75\) とします。
十の位と一の位の数をいれかえてできる \(2\) けたの整数は \(57\) です。
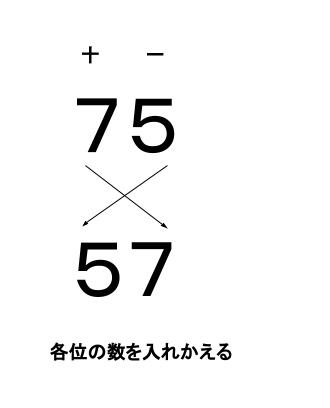
ところで、\(75-57=18\)
\(18\) は \(9\) の倍数なので、確かに成り立っていますね。
2けたの数を文字であらわす
さて、問題の意味をわかったところでどうやって解いていくのか考えていきましょう。
\(2\) けたの整数は、\(10\) から \(99\) まで、\(90\) 個あります。
つまり \(90\) 回調べれば、それで示すこともできるわけです。
しかし、なかなか面倒です。
それに、文字を使って説明しなさい、という解き方の指定もついています。
どのように文字を使って説明できるのか考察していきましょう。
\(2\) けたの整数を \(n\) とおいたとします。
すると、この整数の十の位は?
この整数の一の位は?
どちらも \(n\) で表すことができませんね。
これではうまくいきません。
各位の数字そのものを扱っていきたいので、
つまり、
十の位がいくつなのか知りたい⇒ \(a\) とおこう!
一の位がいくつなのか知りたい⇒ \(b\) とおこう!
となります。
このように未知数をおくやり方は、重要解法テクニックとして身につけてください!!
※使う文字はなんでもかまいません。学校の先生がよく使う文字を使うのが無難です。
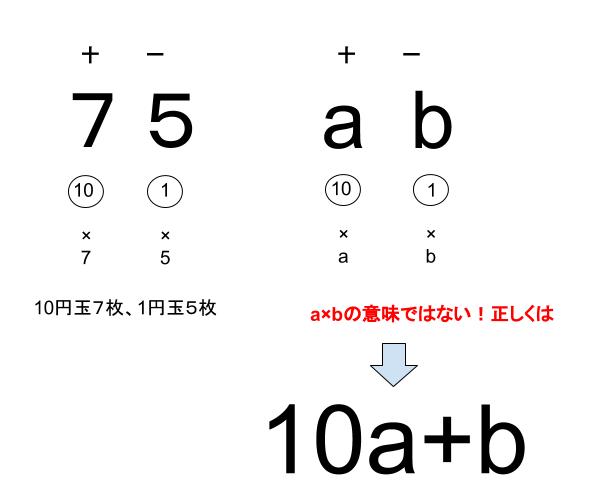
では、もとの\(2\) けたの整数は、\(a\) , \(b\) を用いてどのように表すことができるでしょうか。
\(ab\) とやりたくなってしまいますが、そうではないのです。
これでは、\(a×b\) の意味になってしまいます。
あらためて数の表記について考え直してみましょう。
小学1年生のころからあたりまえのように使用してきた数の表記、
例えば \(75\)(ななじゅうご)
これは \(7\) と \(5\) を並べて書いているわけです。
\(75\) を なな・ごー と電話番号を読むように読まないのはなぜなのか。
\(75\) とは、十が \(7\) つ、一が \(5\) つあることを表してるという「決まり」を無批判に受け入れていたからなのです。
この「決まり」とは異なる決まりで表現するのが、文字式です。
文字式では、並べてかくとかけ算の意味になってしまうので、
もっと丁寧に表現します。
十の位が \(a\) とは、\(10\) が \(a\) 個あるということ
一の位が \(b\) とは、\(1\) が \(b\) 個あるということ
つまり、\(10a+b\) です。
いよいよ問題を解くための準備が整いました。
解答例は以下のようになります。
例題1 問題再掲
\(2\) けたの整数と、その数の十の位の数と一の位の数を入れかえた数との差は、\(9\) の倍数になることを文字を使って説明しなさい。
解答例
整数\(a\),\(b\) を用いて、\(2\) けたの整数は \(10a+b\) と表せる。
この数の十の位の数と一の位の数を入れかえた数は、\(10b+a\) となる。
よって、
\((10a+b)-(10b+a)\)
\(=9a-9b\)
\(=9(a-b)\)
\(a-b\) は整数なので、\(9(a-b)\) は \(9\) の倍数。
よって、\(2\) けた整数と、その数の十の位の数と一の位の数を入れかえた数との差は \(9\) の倍数になる。
スポンサーリンク
