例題1
当たりが \(2\) 本、はずれが \(3\) 本入っているくじの箱がある。この箱からくじを \(2\) 本引くとき、次の確率を求めなさい。
①\(1\) 本くじを引き、引いたくじを箱にもどしてから、もう \(1\) 本くじを引くとき、\(1\) 本当たりの出る確率
②\(1\) 本くじを引き、引いたくじを箱にもどさないで、もう \(1\) 本くじを引くとき、\(1\) 本当たりの出る確率
③\(2\) 本同時にくじをひくとき、\(1\) 本当たりのでる確率
解説
すべてのくじに名前をつけて区別します。
そして、書き出します。
当たり \(2\) 本を \(A,B\)
はずれ \(3\) 本を \(1,2,3\)
と名付けます。
もちろん区別さえできれば、名前はなんでもかまいません。
さて樹形図で書き出していきましょう!
①引いたくじをもどす
引いたくじを箱にもどすので、同じくじを \(2\) 連続で引くこともありますね。
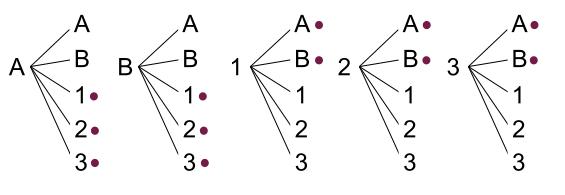
全部で \(25\) 通りあることがわかります。
そして、\(1\) 本当たりがでているのは、●印をつけた \(12\) 通りです。
よって、求める確率は、\(\displaystyle \frac{12}{25}\) です。
全書き出しをしないで、計算で求める
上の樹形図ですが、すべて \(5\) 本に枝分かれしています。
よって、\(1\) 回目に引くくじが \(5\) 通り、\(2\) 回目に引くくじが、\(5\) 通り、
\(5×5=25\)(通り)
と全場合の数を計算で求めることもできます。
しかし、計算で済ませることができるのは、全体像が上の樹形図のようになることが、確実に手にとるようにわかるからこそです。
たくさんの書き出しを経験することで、計算だけで済ませられるようになる日もくるかもしれません。
ところで、\(1\) 本だけ当たりの場合の数は、計算ではどのように求めるのでしょうか。
以下のようになります。
①\(1\) 回目が当たりで、\(2\) 回目がはずれ
\(2×3=6\)(通り)
②\(1\) 回目がはずれで、\(2\) 回目が当たり
\(3×2=6\)(通り)
①と②あわせて、\(6+6=12\)(通り)
いかがでしょうか?
全部書き出した方が楽だな、と感じた人が多いのではないでしょうか?
はい、どんどん全書き出しをしていきましょう!
②引いたくじをもどさない
もちろん樹形図による書き出しです。
\(1\) 回目に引いたくじをもどさないので、\(2\) 回目に引くことはありませんね。
下の図のようになります。
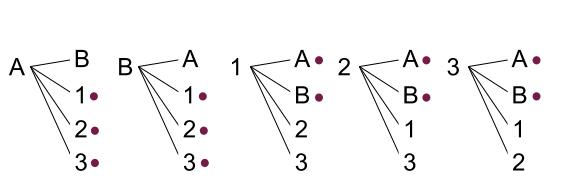
全部で \(20\) 通りあることがわかります。
そして、\(1\) 本当たりがでているのは、●印をつけた \(12\) 通りです。
よって、求める確率は、\(\displaystyle \frac{12}{20}=\displaystyle \frac{3}{5}\) です。
もちろん、慣れてくれば計算で求めてしまってもかまわないです。
③2本同時にくじを引く
○同時に取り出すので、同じくじ \(2\) つを引くことはない。
○同時に取り出すので、順序は関係ない。
つまり、「\(A,B\)」と「\(B,A\)」を区別しない。
これに注意して書き出すと、下の図のようになります。
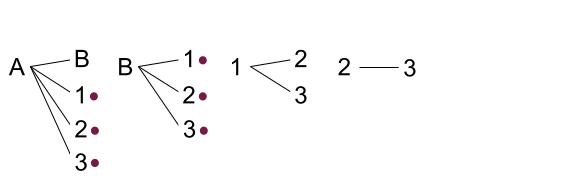
全部で \(4+3+2+1=10\) 通りあることがわかります。
そして、\(1\) 本当たりがでているのは、●印をつけた \(6\) 通りです。
よって、求める確率は、\(\displaystyle \frac{6}{10}=\displaystyle \frac{3}{5}\) です。
2本同時と1本ずつ順に2本は同じ確率
ちなみに \(2\) 本同時に引くときの樹形図は、②の樹形図の半分になっています。
②の樹形図は、「\(1\) 本ずつ順に引くときの樹形図」です。
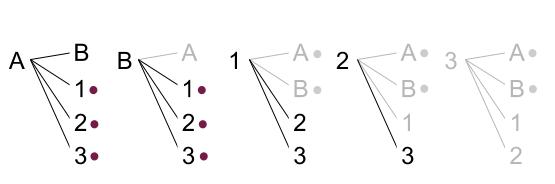
また、②と③で確率が等しいことも偶然ではありません。
\(1\) 本ずつ \(2\) 本引くのと、同時に \(2\) 本引くのと、当たりやすさに違いがないということです。
当たり前ですよね。
スポンサーリンク
