【中学数学】確率・コインの表裏

例題１

$2$ 枚のコインを同時に投げます。
両方表がでる確率を求めなさい。

コインの出方はどのようなものがあるでしょうか。
表を○、裏を×とすると、

$2$ 枚とも表　　○○
$1$ 枚だけ表　　○×
$2$ 枚とも裏　　××

よって、全場合の数は $3$ 通り、
両方表は $1$ 通り、
求める確率は、$\displaystyle \frac{1}{3}$

残念ながら、これは間違いなのです！

なぜなら、「$2$ 枚とも表」がでる出やすさと、
「$1$ 枚表・$1$ 枚裏」がでる出やすさは同じではないからです。
（まさにこの出やすさを数値化したものが確率です）

もっと直感にうったえる例を出すならば、
$10$ 枚のコインを同時に投げてみましょう。
多くの場合、「表が $5$ 枚・裏が $5$ 枚」とか「表が $6$ 枚・裏が $4$ 枚」とかになりそうですよね。
「$10$ 枚とも表」なんて、滅多に出ないであろうことは想像できます。

つまり、「表が $5$ 枚・裏が $5$ 枚」と「$10$ 枚とも表」を等しく $1$ 通り、
と扱ってはいけないことがわかります。

ではどうするのか。
「すべてのコインに名前をつけて、区別する」
のです。
これは、さまざまな場合の数を求めるときに、頻繁に使われます。
必ず覚えておきましょう。

では正しい解答です。
以下のようになります。

$2$ 枚のコインを、$A,B$ とする。
表を〇、裏を×とすると、

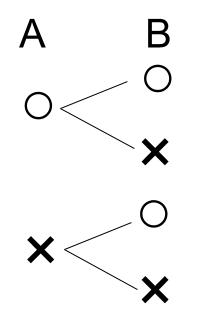
$中学数学・高校受験chu-su- 確率　コイン2枚の表裏　図１$

よって、全場合の数は $4$ 通り、$2$ 枚とも表が出るのは $1$ 通りなので、
求める確率は、$\displaystyle \frac{1}{4}$ となります。

$3$ 枚の硬貨を同時に投げるとき、$1$ 枚が表、$2$ 枚が裏となる確率を求めなさい。

$3$ 枚の硬貨を、$A,B,C$ とします。
表を○、裏を×をして図示します。

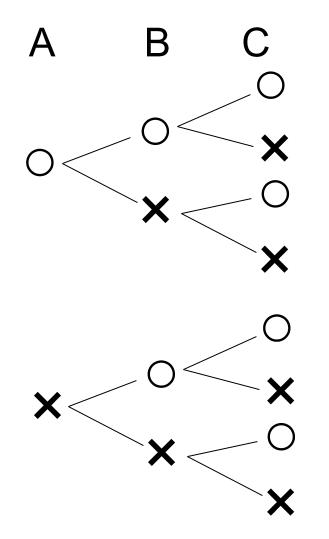
$中学数学・高校受験chu-su- 確率　コイン2枚の表裏　図2$

よって、全場合の数は $8$ 通り、$1$ 枚が表、$2$ 枚が裏となるのは $3$ 通りなので、
求める確率は、$\displaystyle \frac{3}{8}$ となります。