例題1
大小 \(2\) つのさいころを同時に投げます。
出た目の和が \(8\) となる確率はいくらか。
解説
樹形図
樹形図で書きだします。
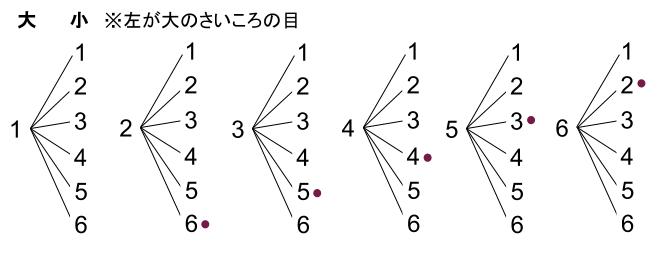
すべての場合の数は、\(6×6=36\) 通り
出た目の和が \(8\) になるのは、●のついた \(5\) 通り。
よって、求める確率は、\(\displaystyle \frac{5}{36}\)
別解 必要な箇所のみ書き出す
上の樹形図で全体像を見ました。
この全体像がきちんと頭に描けるのならば、
全 \(36\) 通りの書き出しをしないで解きましょう。
まず、
\(2\) 個のさいころの目の出方のすべての場合の数は、\(6×6=36\) 通り
これは計算でさっと済ませられますね。
つぎに、出た目の和が \(8\) になるものだけ書き出しで調べます。
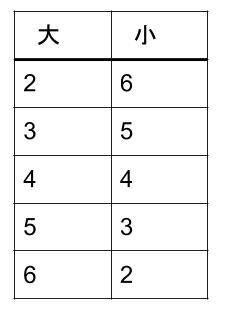
よって、求める確率は、\(\displaystyle \frac{5}{36}\)
別解 表による書き出し
\(2\) 個のさいころの解法として、表による解法も有名です。
結局は、全書き出しによる解法です。
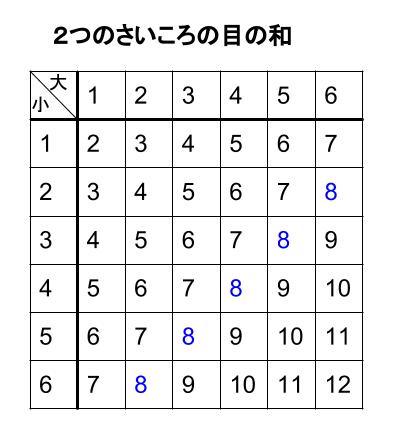
すべての場合の数は、\(6×6=36\) 通り
出た目の和が \(8\) になるのは、青字の \(5\) 通り。
よって、求める確率は、\(\displaystyle \frac{5}{36}\)
例題2
大小 \(2\) つのさいころを同時に投げます。
出た目の積が \(3\) の倍数となる確率はいくらか。
解説
表による書き出し
例題\(1\) で見たように、全 \(36\) 通りを調べるのが基本です。
あとは、いかに省略できるところを省略するかですが・・・
どのような工夫で省略ができるのか。
まったく頭にめぐらないならば、当然書きだします。
樹形図と表、どちらが簡単でしょう。
初学者には表がおすすめです。
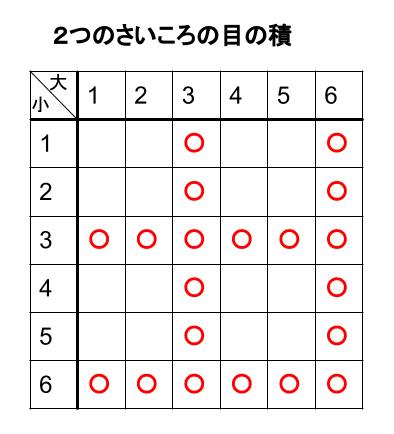
すべての積を計算する必要はありません。
積が \(3\) の倍数になる箇所に〇を入れていきましょう。
積が \(3\) の倍数になるのは、
(\(3\) の倍数)×(整数)
のときです。
全部で、\(20\) 通りあります。
よって、求める確率は、\(\displaystyle \frac{20}{36}=\displaystyle \frac{5}{9}\)
別解 必要な箇所のみ調べる
書き出し量を減らすにはどうすればいいでしょうか。
まず、すべての場合の数は、\(6×6=36\) 通りはよいですね。
ですから、積が \(3\) の倍数になる場合の数さえ求まればOKです。
積が \(3\) の倍数になるのは、上でも確認したとおり、
(\(3\) の倍数)×(整数)のときなので下の樹形図のようになります。
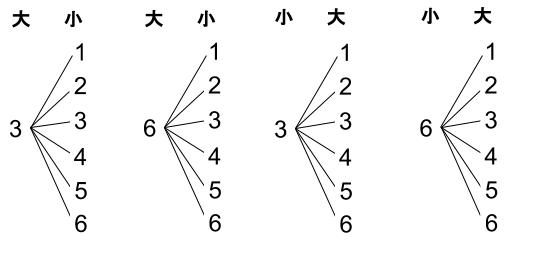
もちろん全体像がわかった時点で書き出しをやめて、
\(6×4=24\) (通り)
と計算で済ませてしまっても構いません。
しかし、これで終わりではありません。
この \(24\) 通りの中には、\(2\) 重に数えてしまっているものがあるのです。
下図の同じ記号をつけた \(4\) 通りが、\(2\) 重になっているものです。
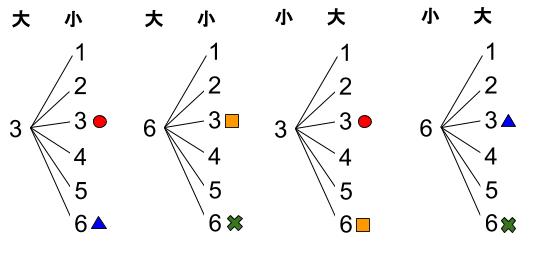
よって \(2\) つの目の積が \(3\) の倍数になるのは、\(24-4=20\)(通り)です。
よって、求める確率は、\(\displaystyle \frac{20}{36}=\displaystyle \frac{5}{9}\)
いかがでしょう。
楽をしようとしてみても、上手に楽ができないものですね。
たくさん経験を積んで、省略の仕方や、そもそも省略の解法は簡単なのかなど、
\(1\) つ \(1\) つ学習していくしか道はありません!!
最も大切な教えは
「全書き出しをすることを嫌がるな!」
です。
全書き出しの経験をしないと、全体像がつかめないからです。
全体像をつかんでいない人に、省略の解法は見えてきません。
\(1\) つ \(1\) つコツコツとやっていく姿勢が大事です。
スポンサーリンク
