例題1
次の連立方程式を解きなさい。
$\left\{ \begin{array}{@{}1} 0.6x-1.2y=3\\ 2x+0.8y=0.4 \end{array} \right. $
解説
\(1\) 次方程式を解くときと同じです。
等式の両辺を \(10\) 倍、\(100\) 倍して小数点がない式にしてしまいましょう。
$\left\{ \begin{array}{@{}1} 0.6x-1.2y=3 ・・・①\\ 2x+0.8y=0.4 ・・・② \end{array} \right. $
①\(×10\)
\(6x-12y=30\)
この式の両辺を \(6\) で割って、
\(x-2y=5\)・・・①´
②\(×10\)
\(20x+8y=4\)
この式の両辺を \(4\) で割って、
\(5x+2y=1\)・・・②´
①´と②´を連立して解きます。
①´+②´
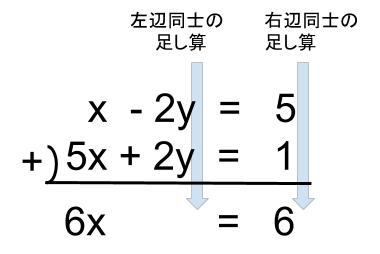
よって、\(x=1\)
これを①´に代入すると、
\(1-2y=5\)
\(y=-2\)
別解
「小数点をはずして、整数で計算する」
これはルールではありません。小数のまま計算しても構いません。
$\left\{ \begin{array}{@{}1} 0.6x-1.2y=3 ・・・①\\ 2x+0.8y=0.4 ・・・② \end{array} \right. $
②\(×0.3\)
\(0.6x+0.24y=0.12\)・・・③
①´と③を連立して解きます。

よって、\(y=-2\)
これを①に代入すると、
\(0.6x+2.4=3\)
\(x=1\)
例題2
次の連立方程式を解きなさい。
$\left\{ \begin{array}{@{}1} \displaystyle \frac{1}{2}x+\displaystyle \frac{3}{4}y=8\\ \displaystyle \frac{x}{4}-\displaystyle \frac{y}{3}=-\displaystyle \frac{1}{4} \end{array} \right. $
解説
等式の両辺に同じ数をかけて、整数だけの式にしてしまいましょう。
$\left\{ \begin{array}{@{}1} \displaystyle \frac{1}{2}x+\displaystyle \frac{3}{4}y=8 ・・・①\\ \displaystyle \frac{x}{4}-\displaystyle \frac{y}{3}=-\displaystyle \frac{1}{4} ・・・② \end{array} \right. $
①\(×4\)
\(2x+3y=32\)・・・①´
②\(×12\)
\(3x-4y=-3\)・・・②´
これを連立します。
$\left\{ \begin{array}{@{}1} 2x+3y=32 ・・・①´\\ 3x-4y=-3 ・・・②´ \end{array} \right. $
ここから先は、加減法でも代入法でもなんでもよいです。
連立方程式を解けばよいのです。
$\left\{ \begin{array}{@{}1} x=7\\ y=6 \end{array} \right. $
別解
もちろん、整数に直さないでも良いんです。
①式\(÷2\) で②と \(x\) の係数がそろうので、このまま加減法で解いても構いません。
$\left\{ \begin{array}{@{}1} \displaystyle \frac{1}{4}x+\displaystyle \frac{3}{8}y=4・・・①÷2\\\displaystyle \frac{x}{4}-\displaystyle \frac{y}{3}=-\displaystyle \frac{1}{4}・・・② \end{array} \right. $
これを解いて、
$\left\{ \begin{array}{@{}1} x=7\\ y=6 \end{array} \right. $
スポンサーリンク
