例題1
\(A,B,C,D\) の \(4\) 人が、リレーのチームを組む。走る順番をくじで決めるとき、次の確率を求めさない。
① \(A\) がアンカーになる確率
② \(A\) の次に \(B\) が走る確率
解説
樹形図を書きます。
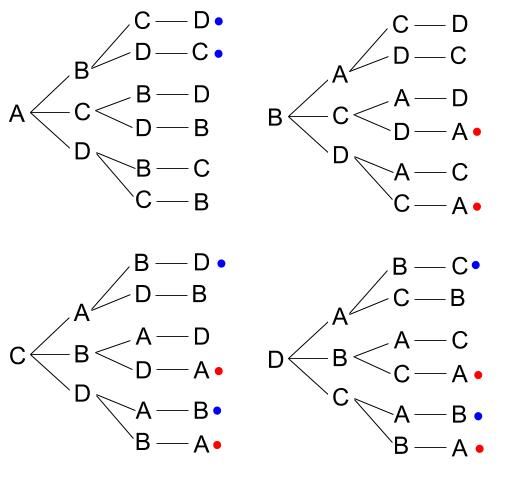
よって、全場合の数は \(24\) 通りです。
① \(A\) がアンカーになる確率
\(A\) がアンカーになるのは、赤丸の \(6\) 通りです。
よって、もとめる確率は、\(\displaystyle \frac{6}{24}=\displaystyle \frac{1}{4}\) です。
② \(A\) の次に \(B\) が走る確率
\(A\) の次に \(B\) が走るのは、青丸の \(6\) 通りです。
よって、求める確率は、\(\displaystyle \frac{6}{24}=\displaystyle \frac{1}{4}\) です。
例題2
そうじ当番 \(2\) 人を、男子 \(2\) 人、女子 \(3\) 人の計 \(5\) 人の中からくじびきで決めるとき、次の確率を求めなさい。
①男女 \(1\) 人ずつが選ばれる確率
②女子 \(2\) 人が選ばれる確率
解説
人に名前をつけて区別します。場合の数を求めるための重要暗記事項です。
男子を \(A,B\)
女子を \(1,2,3\)
として、樹形図を書きます。
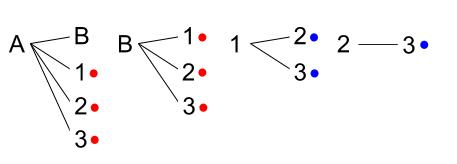
よって、全場合の数は \(4+3+2+1=10\) 通りです。
①男女1人ずつが選ばれる確率
男女 \(1\) 人ずつが選ばれるのは、赤丸の \(6\) 通りです。
よって、求める確率は、\(\displaystyle \frac{6}{10}=\displaystyle \frac{3}{5}\) です。
②女子2人が選ばれる確率
女子 \(2\) 人が選ばれるのは、青丸の \(3\) 通りです。
よって、求める確率は、\(\displaystyle \frac{3}{10}\) です。
例題3
そうじ当番 \(2\) 人を、男子 \(2\) 人、女子 \(3\) 人の計 \(5\) 人の中からくじびきで決めます。赤いくじを引いた \(1\) 人がほうき、黒いくじを引いた \(1\) 人がぞうきんとするとき、男子がほうき、女子がぞうきんの当番になる確率を求めなさい。
解説
男子を \(A,B\)
女子を \(1,2,3\)
として、樹形図を書きます。
赤を引いたのは誰なのか、\(5\) 通りありえますね。
例えば \(A\) が赤を引いたとき、黒を引いたのは \(B,1,2,3\) の \(4\) 通りありえます。
以下の図のようになりますね。
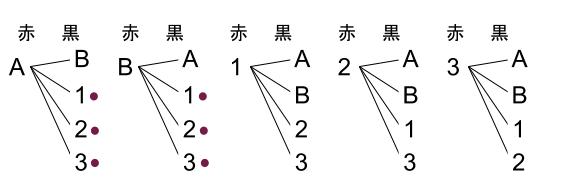
よって、全場合の数は \(20\) 通りです。
男子がほうき、女子がぞうきんの当番になるのは、●丸の \(6\) 通りです。
よって、求める確率は、\(\displaystyle \frac{6}{20}=\displaystyle \frac{3}{10}\) です。
スポンサーリンク
