格子点を読み取る
\(1\) 次関数のグラフを読みとることも大切です。
これも比例と似ている部分が多いです。
例題1
次の直線の式を求めなさい
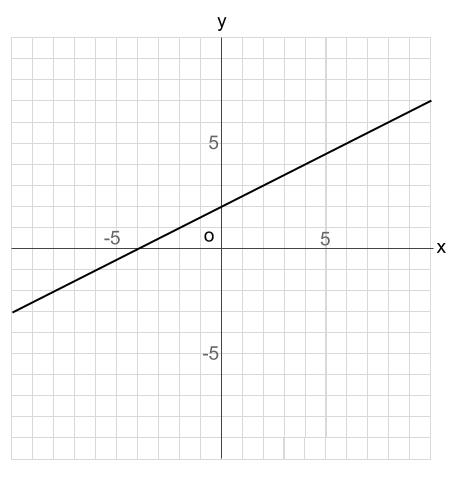
解答
直線の式を求めなさい
ときたら、
\(y=ax+b\)
の \(a\) と \(b\) を求めること
であるとまず理解してください。
これは「基本の型」です。
しっかりと理解・暗記をしましょう。
\(a\) は傾き(変化の割合)
\(b\) は切片でした。
わずわらしい計算をしなくとも、グラフを読みとるだけで
\(a\) や \(b\) が求まることもあります。
切片を読み取る
この例題では、切片が読めます。計算はいりませんね。
切片は \(2\) です。
よって、\(b=2\) です。
傾きは、通る2点から
傾きは、直線が通る \(2\) 点から読みとれます。
切片以外に、もう \(1\)つ格子点を探すと \((2,3)\) があります。
傾きは、\(\displaystyle \frac{yの増加量}{xの増加量}\) なので \(\displaystyle \frac{1}{2}\) です。
つまり、\(a=\displaystyle \frac{1}{2}\) です。

よって、求める直線の式は
\(y=ax+b\) に、\(a=\displaystyle \frac{1}{2},b=2\) を代入して、
\(y= \displaystyle \frac{1}{2}x+2\)
切片が読みとれないとき
例題2
次の直線の式を求めなさい
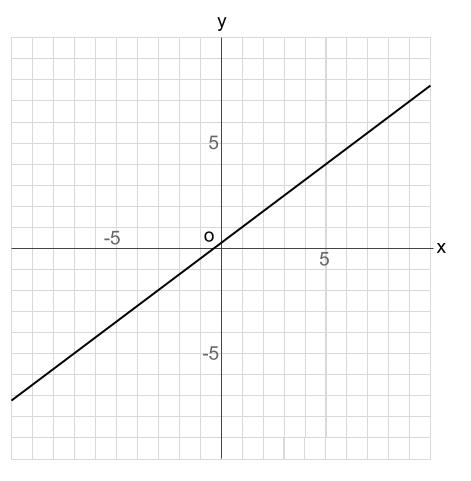
解説
切片がよめませんね。
このようなときは、計算で求めることになります。
傾きは、通る2点から
直線が通る格子点を \(2\) 点を探します。
\((1,1)\)
と
\((5,4)\)
がみつかります。
よって傾きは\(\displaystyle \frac{3}{4}\) とわかりました。
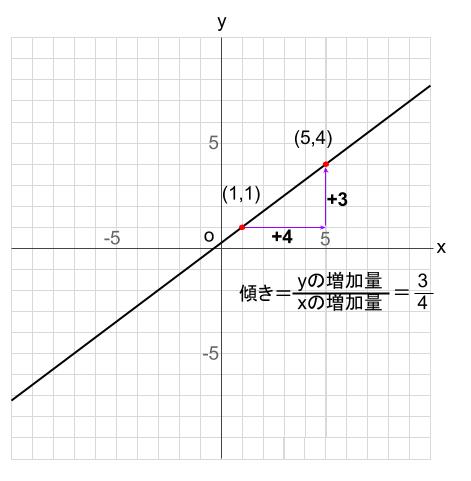
よって、もとめる直線の式は
\(y=\displaystyle \frac{3}{4}x+b\)
であることがわかります。
あとは \(b\) を決定します。
通る点を代入
この直線の式に、この直線が通る点を代入すれば、 \(b\) の \(1\) 次式になり、\(b\) が求まります。
\((1,1)\) でも \((5,4)\) でもなんでもかまいません。
例えば \((1,1)\) を代入すると、
\(1=\displaystyle \frac{3}{4}+b\)
より、\(b=\displaystyle \frac{1}{4}\) と求まります。
よって、\(y=\displaystyle \frac{3}{4}x+\displaystyle \frac{1}{4}\)
別解
通る \(2\) 点をそれぞれ直線の式 \(y=ax+b\) に代入して、連立方程式で \(a\) と \(b\) を求めることもできます。
\((1,1)\) を代入して
\(1=a+b\)
\((5,4)\) を代入して
\(4=5a+b\)
これを解いて \(a=\displaystyle \frac{3}{4}\),\(b=\displaystyle \frac{1}{4}\)
あたりまえですが、これを答えとしてはいけませんよ。
求めよ、と指示されているのは直線の式です。
つまり、\(y=ax+b\) の形で答えなくてはなりませんね。
よって、\(y=\displaystyle \frac{3}{4}x+\displaystyle \frac{1}{4}\)
スポンサーリンク
