2つの直線が交わる
例題1 図示して交点を求める
\(2\) 直線
\(y=x-1\)
\(y=-\displaystyle\frac{1}{2}x+5\)
の交点の座標を求めなさい。
解説
図示してみると・・・
\(2\) つの直線を図示してみましょう。
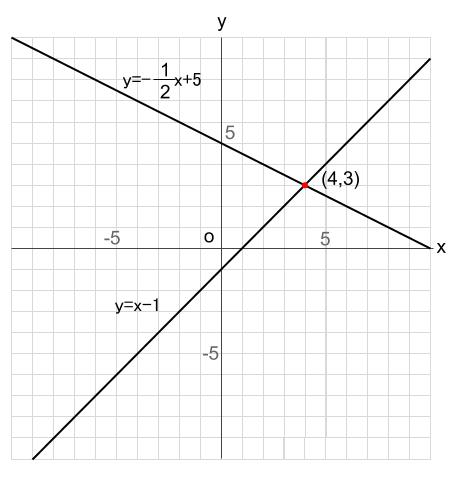
\((4,3)\) で交わることが確かめられます。
よって求める交点は、\((4,3)\) です。
交点を計算で求める
ところで \(2\) 直線の交点は、計算で求めることも可能です。
\(y=x-1\) を満たす\(x\),\(y\) の組が無数にあり、
\(y=-\displaystyle\frac{1}{2}x+5\) を満たす\(x\),\(y\) の組が無数にあり、
その中で、共通なものを探す、ということです。
これは・・・
連立方程式の解を求めることと同じです!
つまり、\(2\) 直線の交点は、
連立方程式
$\left\{ \begin{array}{@{}1} y=x-1\\ y=-\displaystyle\frac{1}{2}x+5 \end{array} \right. $
の解を求めることと一致します。
さきほど図示することで得た交点の座標 \((4,3)\) が、
計算で求まります。
図示してみても、交点が格子点(\(x\) 座標も \(y\) 座標も整数の点)である保障もありません。
\(2\) 直線の交点は、連立方程式で求める、と覚えましょう。
例題2 計算で交点を求める
\(2\) つの直線が右図のように点 \(P\) で交わっている。このとき、次の問いに答えなさい。
①直線 \(L\) の式を求めなさい。
②直線 \(M\) の式を求めなさい。
③交点 \(P\) の座標を求めなさい。
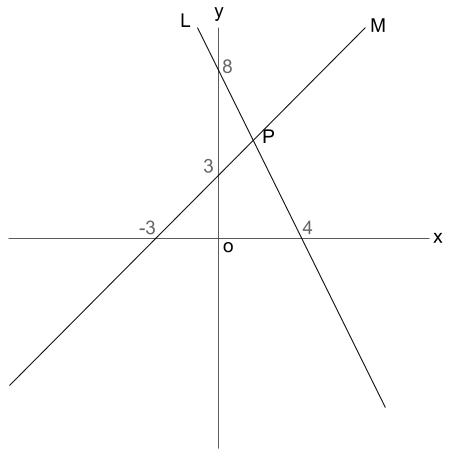
解説
①直線 \(L\) の式を求めなさい
①直線 \(L\) の切片は\(8\) 、傾きは
\(\displaystyle \frac{yの増加量}{xの増加量} = \displaystyle \frac{-8}{4} = -2 \)
よって、直線 \(L\) の式は
\(y=-2x+8\)
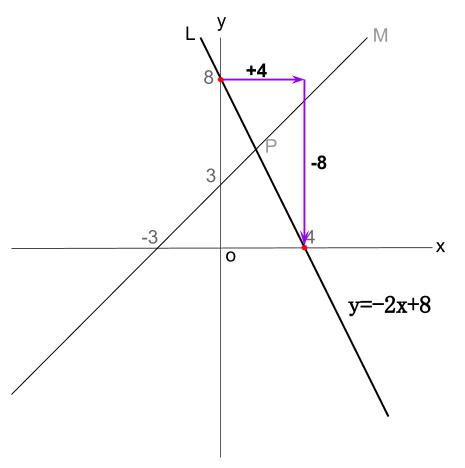
②直線 \(M\) の式を求めなさい
② 直線 \(M\) の切片は \(3\) 、傾きは
\(\displaystyle \frac{yの増加量}{xの増加量} = \displaystyle \frac{3}{3} = 1 \)
よって、直線 \(M\) の式は
\(y=x+3\)
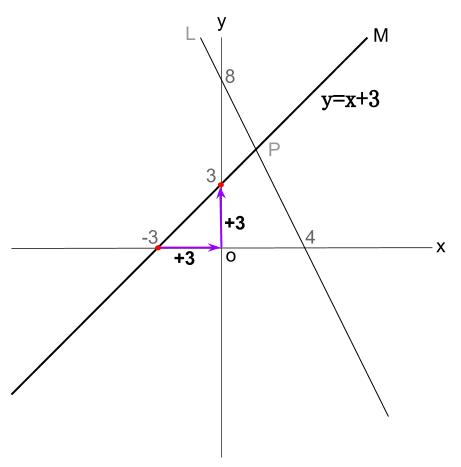
③交点 \(P\) の座標を求めなさい
③\(2\) 直線の式を連立方程式として解きます。
$\left\{ \begin{array}{@{}1} y=-2x+8\\ y=x+3 \end{array} \right. $
これを解いて
$\left\{ \begin{array}{@{}1} x= \displaystyle \frac{5}{3} \\ y= \displaystyle \frac{14}{3} \end{array} \right. $
よって、交点 \(P\) の座標は
\(( \displaystyle \frac{5}{3}, \displaystyle \frac{14}{3})\)
スポンサーリンク
