三角形の合同の証明の利用
四角形 \(ABCD\) が平行四辺形であることを示すために、
辺の長さ、角の大きさが等しいことを示したいときがあります。
これを示すために、
「三角形の合同を証明し、そこから示す」
ということがあります。
例題1
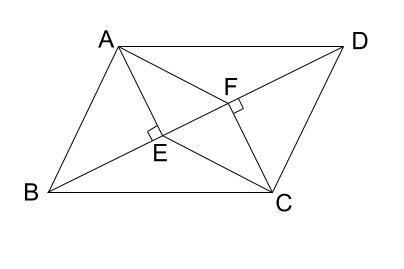
平行四辺形 \(ABCD\) の頂点 \(A,C\) から対角線 \(BD\) に垂線 \(AE,CF\) をひく。
このとき、四角形 \(AECF\) は平行四辺形であることを証明しなさい。
解説
垂線を引いて作られた四角形が平行四辺形であることを示す問題です。
当然ですが、この垂線の図形的性質から証明されるはずです。
垂直という角度の情報から、
\(AE /\!/ CF\)
が言えます。
錯角が等しいので平行、ということです。
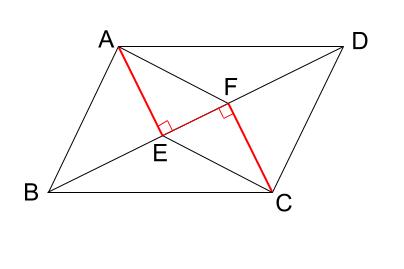
よって、あと何が成り立てば
平行四辺形になるための \(5\) 条件のいずれかに該当するのか、
と考えましょう。
\(AE=CF\) が示せれば、\(1\) 組の対辺が平行でその長さが等しい
が言えます。
※ \(AF=EC\) が示せれば、「\(2\) 組の対辺がそれぞれ等しい」になりますが、
これは簡単には示せそうにないですね・・・
\(AE=CF\) は、下の図の直角三角形の合同が示せればいえます。
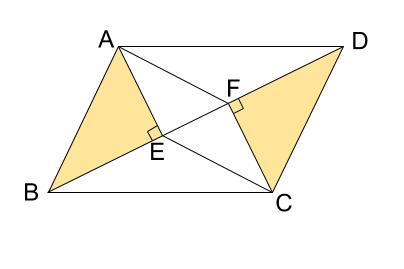
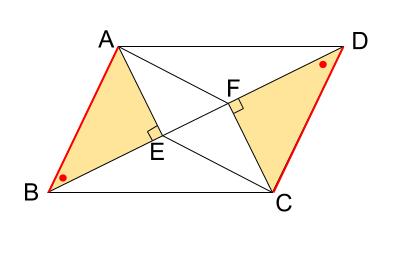
斜辺 \(AB=CD\)
鋭角 \(\angle ABE=\angle CDF\)
ですね。
解答
仮定より、\(\angle AEF=\angle CFE\)
なので、錯角が等しいことから
\(AE /\!/ CF\)・・・①
仮定より、四角形 \(ABCD\) が平行四辺形なので
\(AB=CD\)・・・②
\(\angle ABE=\angle CDF\)・・・③
②、③より
直角三角形の斜辺と \(1\) つの鋭角がそれぞれ等しいので
\(\triangle ABE \equiv \triangle CDF\)
合同な図形の対応する辺の長さは等しので、
\(AE=CF\) ・・・④
①、④より\(1\) 組の対辺が平行でその長さが等しいので
四角形 \(AECF\) は平行四辺形である。
例題2
平行四辺形 \(ABCD\) の辺 \(BC\) の中点を \(E\) とし、 \(AE,DC\) それぞれの延長戦の交点を \(F\) とする。このとき、四角形 \(ABFC\) は平行四辺形であることを証明しなさい。
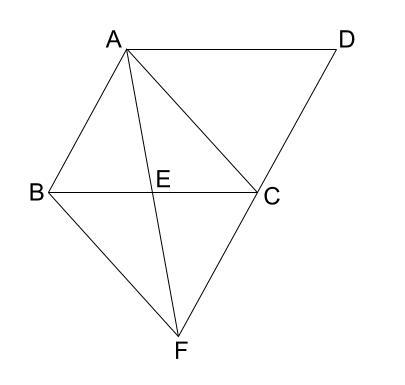
解説
示したい四角形の対角線が与えられていますので
第一候補は
・対角線がそれぞれの中点で交わる
です。
しかも、\(1\) つは仮定で与えらえています。\(BE=CE\) です。
よって、もう \(1\) つの対角線が中点で交わっていることを
示すことが目標です。
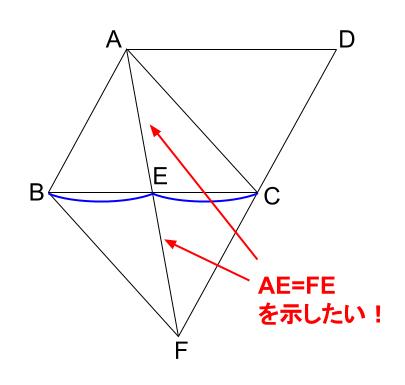
やはり、三角形の合同を示すことで達成できますね。
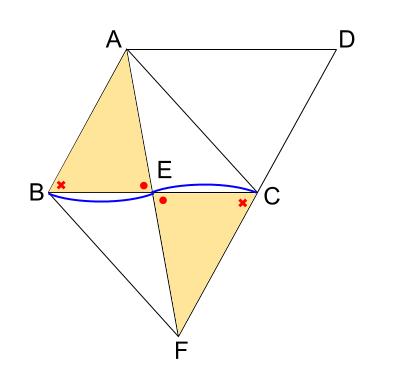
下図のクリーム色の三角形の合同です。
〇の角が等しいのは対頂角
×の角が等しいのは平行線の錯角
\(1\) 辺とその両端の角がそれぞれ等しいので合同です。
解答
仮定より、\(BE=CE\)・・・①
仮定より、\(AB /\!/ DF\) なので
平行線の錯角は等しいので、\(\angle ABE=\angle FCE\)・・・②
対頂角は等しいので、\(\angle BEA=\angle CEF\)・・・③
①、②、③より、\(1\) 辺とその両端の角がそれぞれ等しいので
\(\triangle ABE \equiv \triangle FCE\)
合同な図形の対応する辺の長さは等しいので
\(AE=FE\)・・・④
①、④より対角線がそれぞれの中点で交わるので
\(ABFC\) は平行四辺形である。
