連立方程式・加減法
連立方程式の解を、すっきりと求めるための手順は確立されています。
- 加減法
- 代入法
の \(2\) つです。
まずは加減法を見ていきましょう。
連立方程式の解き方(加減法)
\(2\) つの方程式の両辺を、足したり引いたり〈加減)することで、\(1\) つの文字を消すことができる!
これが加減法です。
具体例で学習していきましょう。
例題1
次の連立方程式を解きなさい。
$\left\{ \begin{array}{@{}1} x+4y=12・・・①\\ x+2y=10・・・② \end{array} \right. $
同じ符号の文字は引く
\(①-②\)で、 \(x\) の項が消えます。

よって、\(y=1\) と求まります。
これを、①でも②でもどちらでもよのですが、代入すれば \(x\) の \(1\) 次方程式になります。
①に代入すると
\(x+4×1=12\)
より、\(x=8\)
例題2
次の連立方程式を解きなさい。
$\left\{ \begin{array}{@{}1} x+3y=7・・・①\\ -x+2y=8・・・②\end{array} \right. $
異なる符号の文字は足す
\(①+②\)で、 \(x\) の項が消えます。
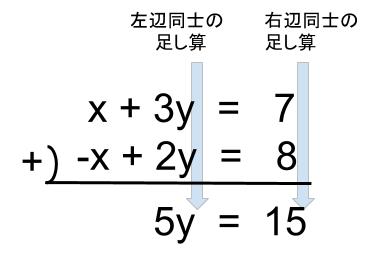
よって、\(y=3\) と求まります。
これを、①でも②でもどちらでもよのですが、代入すれば \(x\) の \(1\) 次方程式になります。
①に代入すると
\(x+3×3=7\)
より、\(x=-2\)
例題3
次の連立方程式を解きなさい。
$\left\{ \begin{array}{@{}1} -3x+4y=4 ・・・①\\ 5x-2y=26・・・② \end{array} \right. $
1つの式をN倍して、係数をそろえる
このままでは、\(2\) つの式を足しても引いても、文字を \(1\) つ消すことはできません。
足したり引いたりして、文字が消えるためには、係数が同じ値である必要があります。
(符号は違っていて可。同符号なら引いて、異符号なら足して消すことができます)。
\(2\) つ目の式、\(5x-2y=26\) を \(2\) 倍すると
\(10x-4y=52\)
となり、\(y\) の係数がそろいました。
\(2\) つの式を足すことで、\(y\) の項を消すことができます。

よって、\(x=8\)
これを①に代入すると
\(-3×8+4y=4\)
\(y=7\)
例題4
次の連立方程式を解きなさい。
$\left\{ \begin{array}{@{}1} 5x-2y=12\\ 3x+5y=1 \end{array} \right. $
2つの式をN倍して、係数をそろえる
どちらの式を何倍すれば、\(x\) の係数をそろえられるのでしょうか。
あるいは、\(y\) の係数をそろえられるのでしょうか。
\(1\) つ目の式を \(3\) 倍、\(2\) つ目の式を \(5\) 倍することで、\(x\) の係数をそろえることができます。
\(15x-6y=36\)
\(15x+25y=5\)
この \(2\) 式の差を取ります。

よって、\(y=-1\) と求まります。
これを用いて
\(x=2\)
と求まります。
スポンサーリンク
