【中学数学】２元１次方程式と連立方程式

２元１次方程式

２元１次方程式とは

$x+2y=9$

このように、$2$ 種類の文字の項がある $1$ 次式を、方程式と見た場合 $2$ 元 $1$ 次方程式といいます。
※関数とみれば $1$ 次関数（次の章で学びます）です。あまり言葉にこだわる必要はありません。

等式の変形をすることで
$x+2y=9$
$2y=-x+9$
$y=-$$\frac{1}{2}$$x+$$\frac{9}{2}$

など、さまざまに形をかえることができますが、
すべて同じ方程式です。

２元１次方程式の解

$2$ 元 $1$ 次方程式の解は無限に存在します。

解とは何か、覚えていますか？
解とは、その方程式を成り立たせる値のことです。

$x+2y=9$　の解の１つは　$x=1,y=4$ です。
このように、 $x$ と $y$ の値の組が解になります。

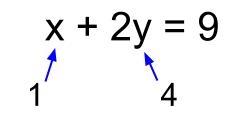
先ほど解は無限に存在すると書きました。
確認しておきましょう。
例えば
$x=2$ のとき、$y=3.5$
$x=3$ のとき、$y=3$
$x$ は整数である必要はありません。
$x=0.1$ のとき、$y=4.45$

その他、どんな $x$ の値に対しても、この方程式を成り立たせる $y$ の値がありますね。

つまりこの方程式の解は無限に存在します。

連立方程式

連立方程式とは

方程式の組を連立方程式といいます。

連立方程式の解は、組をつくった方程式の共通の解となります。

例題

次の連立方程式を解きなさい
$\left\{ \begin{array}{@{}1} 2x+y=3\\ 3x-y=7 \end{array} \right.$

解説

$2$ つの $2$ 元 $1$ 次方程式が与えられました。それぞれ、ア、イと名付けます。
ア：$2x+y=3$
イ：$3x-y=7$

アを満たす解は無限にあります。
イを満たす解も無限にあります。
アの解であり、かつイの解であるものがたった１つあります。

このアとイに共通の解が、連立方程式の解です。

アの解の一部を調べてみると

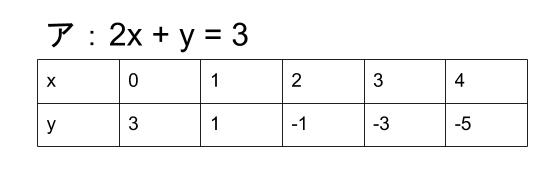
イの解の一部を調べてみると

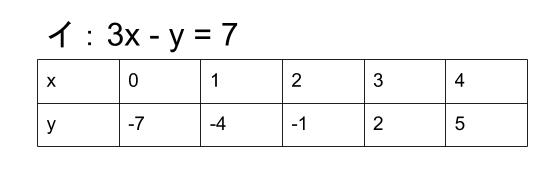
アの解であり、かつイの解であるものを探します。
$x=2,y=-1$ がアとイの共通の解としてみつかりました。
連立方程式の解は、$x=2,y=-1$です。
また解を下のようにまとめる表記もよくあります。
$\left\{ \begin{array}{@{}1}x=2\\ y=-1 \end{array} \right.$

さて、連立方程式の解は上のようにひたすら探すしかないのでしょうか？
うまく求める方法はないのでしょうか。

もちろんあります。加減法と代入法という２つの方法をこれから学習していきましょう。

スポンサーリンク

• 次のページ 連立方程式・加減法