例題1
次の \(1\) 次関数のグラフをかきなさい。
\(y=\displaystyle \frac{2}{3}x-1\)
解説
\(1\) 次関数のグラフのかきかたは以下の \(2\) つをまず覚えましょう。
- \(1\) 次関数のグラフは必ず直線になる。
- 「直線は、通る \(2\) 点が定まれば \(1\) つに定まる」ので,直線が通る \(2\)点を求める。
グラフをかく手順
よって、簡単にまとめると
ア:\(y=\displaystyle \frac{2}{3}x-1\) が通る \(2\) 点を求めます。
イ:その \(2\) 点を結ぶ直線をピーっと引けばOKなのです。
順に見ていきましょう。
直線が通る2点を求める
ア:\(y=\displaystyle \frac{2}{3}x-1\) が通る \(2\) 点を求めます。
\(y=\displaystyle \frac{2}{3}x-1\) が通る点は無限にあるので、
そのうちのどの \(2\) 点を求めても構いません。
どの \(2\) 点でも構わないのですが、
簡単にかくならこれでしょ!
というやり方は確立されています。
それを見ていきましょう。
まず、直線と \(y\) 軸との交点を求めましょう。
これは、\(x\) 座標が \(0\) となるときなので、とても簡単に求めることができます。
\((0,-1)\) ですね。
この \(y\) 座標は、はじめの \(1\) 次関数の式に表れています。
\(y=\displaystyle \frac{2}{3}x-1\)
の式の最後の \(-1\) の部分です。
これを切片といいます。
しっかり暗記しましょう。
これは暗記しないとまずい語句です。
さて、もう \(1\) 点、\(y=\displaystyle \frac{2}{3}x-1\) が通る点を求めます。
\(x\) 座標も \(y\) 座標も整数となる点、格子点を求めます。
そうでないと、グラフがかけないですからね
\(x=3\) のときに \(y\) が整数になります(分数の分母と同じ \(x\)座標です)
このとき \(y=1\) なので、下のグラフのようになります。
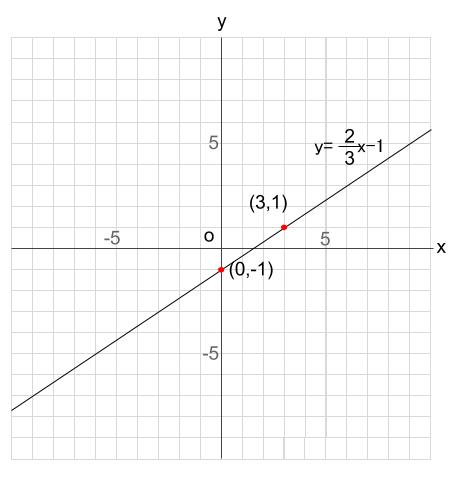
この \((3,1)\) なんですけど、計算で求めたとも言えますが
式の
\(y=\displaystyle \frac{2}{3}x-1\)
から図形的に得ることもできるのです。
\((0,-1)\) から \((3,1)\) まで、
右に \(+3\) の間に、上に \(+2\) 進んでいます。
この \(+3\) と \(+2\) は、直線の式 \(y=\displaystyle \frac{2}{3}x-1\)
の \(x\) の項の係数に表れています。
この\(\displaystyle \frac{2}{3}\) は
直線の傾きを示していると言えます。
直線が通る2点を結ぶ
イ:\(2\) 点を ぴーっと引く で理論上はOKなんですけど・・・
定規が微妙にずれちゃったりするわけですね・・・
だから、この直線は必ずここを通るし、私はそれが分かっている!
と採点者にアピールすることが重要になります。
比例のグラフをかくときと同じです。
よって、右に \(+3\) の間に 上に \(+2\) をくりかえし、通るべき格子点をとっていくことが
おすすめです。
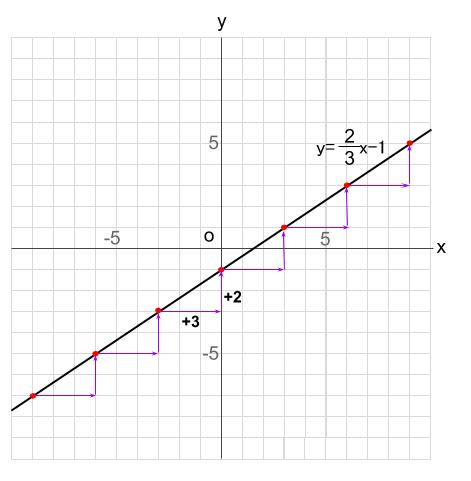
変化の割合 = 傾き
1次関数 \(y=ax+b\) において、
\(a\) は、直線の傾きを表していることを上で見ました。
この \(a\) には別名があり、変化の割合といいます。
変化の割合とは、グラフがどのように変化しているのかを示す値で、
\(変化の割合=\displaystyle \frac{yの増加量}{xの増加量}\)
で定義されます。
\(1\) 次関数においては、変化の割合は一定で、常に \(a\) と等しいのです。
スポンサーリンク
