例題1
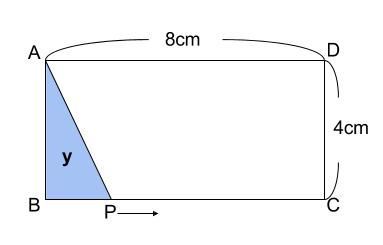
下の図の長方形 \(ABCD\) の辺上を、点 \(P\) が \(B\) を出発し、\(C,D\) を通って \(A\) まで、\(1\) 秒間に \(1cm\) の一定の速さで動きます。点 \(P\) が出発してから \(x\) 秒後の三角形 \(ABP\) の面積を \(ycm^2\) とします。次の問いに答えなさい。
(1)点 \(P\) が\(BC\) 上を動くとき、\(y\) を \(x\) の式で表しなさい。また、\(x\) の変域を求めなさい。
(2)点 \(P\) が \(CD\) 上を動くとき、\(y\) を \(x\) の式で表しなさい。また、\(x\) の変域を求めなさい。
(3)点 \(P\) が \(DA\) 上を動くとき、\(y\) を \(x\) の式で表しなさい。また、\(x\) の変域を求めなさい。
(4)点 \(P\) が \(B\) から \(A\) まで動くとき、\(y\) と \(x\) の関係を表すグラフをかきなさい。
解説
動点の問題は、一度じっくりと向き合って、完璧に理解することが重要です。
そして、ポイントをつかんでさえしまえば、今後はスラスラと解くことができるようになります。
とにかく一度、じっくりとゆっくりと、完璧な理解を目指しましょう。
(1)点 \(P\) が\(BC\) 上を動くとき、\(y\) を \(x\) の式で表しなさい。また、\(x\) の変域を求めなさい
まず、この問題で何が起こっているのか、何が問われているのか、を把握しましょう。
点 \(P\) が出発してから、\(1\) 秒後、\(2\) 秒後、\(3\) 秒後・・・と図示してみましょう。
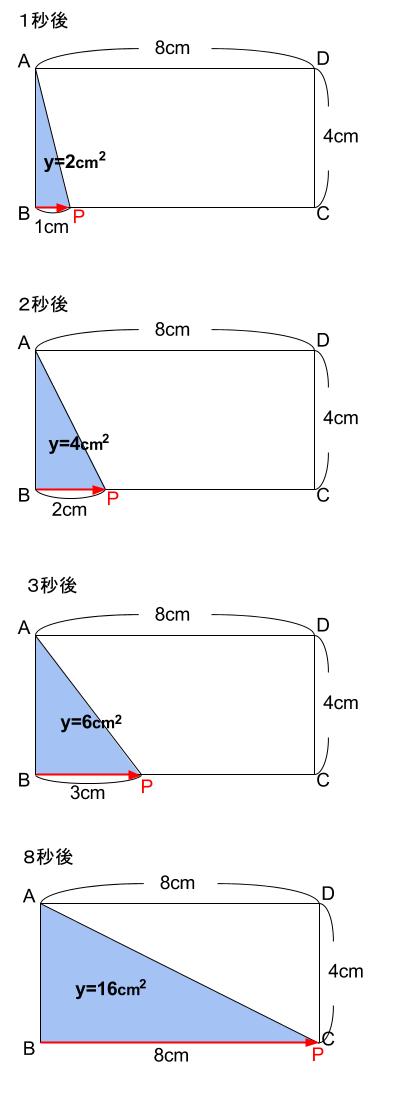
\(P\) が時間とともに、右に移動していき、三角形 \(ABP\) の面積がどんどん増えていっている様子がわかります。\(8\) 秒後、点 \(C\) につくまでをグラフに表してみましょう。
グラフをかくのは(4)ですが、そんな順番なんて関係ありません。どんどんグラフをかいてしましましょう。\(x=0\) のとき、\(y=0\) もあたりまえですね。
これらの点は、直線で結んでしまってよいですね。
つまり、三角形 \(ABP\) の面積は、一定の割合で増加しているということです。
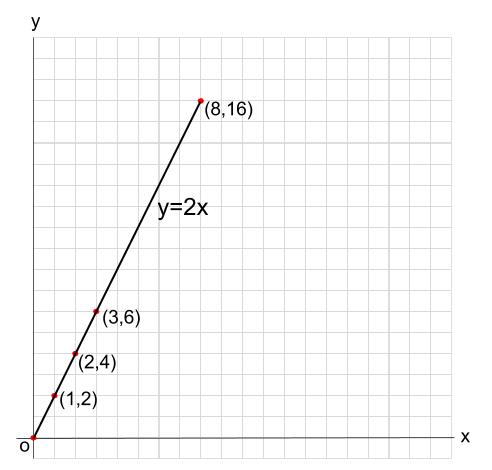
この直線の式を求めれば、これが(1)の答えになります。
傾きは \(2\)、切片は \(0\) なので、\(y= 2x\), \(0 \leqq x \leqq 8\)
と求まりました。
別解
ちなみに、次のような解法もあります。とても大事ですので必ずこちらも理解しておいてください。
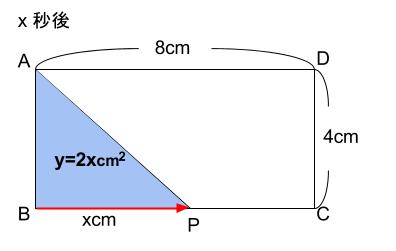
\(x\) 秒後の三角形 \(ABP\) の底辺は、\(xcm\) なので、このときの 面積 \(y\) は
\(y=x×4÷2=2x\)
グラフから得た式と、まったく同じ式が得られましたね。
(2)点 \(P\) が \(CD\) 上を動くとき、\(y\) を \(x\) の式で表しなさい。また、\(x\) の変域を求めなさい
点 \(P\) が \(CD\) 間を動くときの図示をしてみましょう。
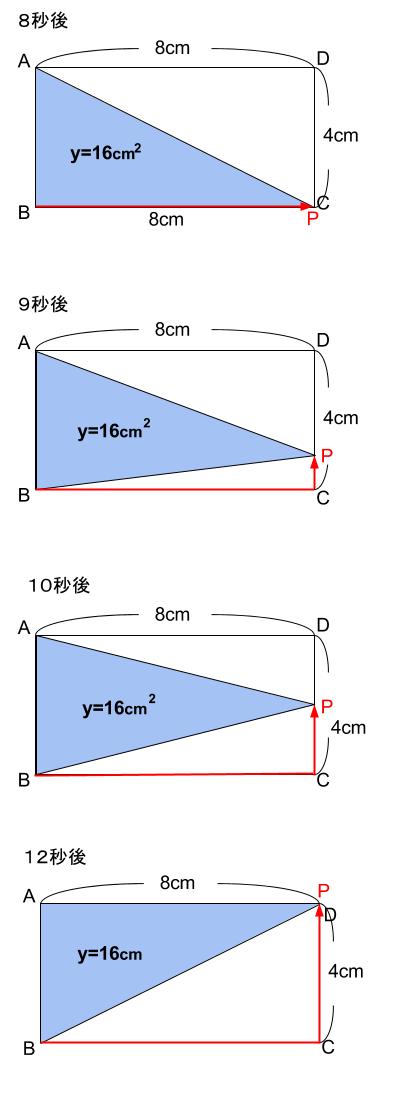
この間は、面積が一定 \(16cm^2\) で変化ありません。これをグラフにかき足します。
このグラフの式は、\(y=16\) 、\(8 \leqq x \leqq 12\)です。
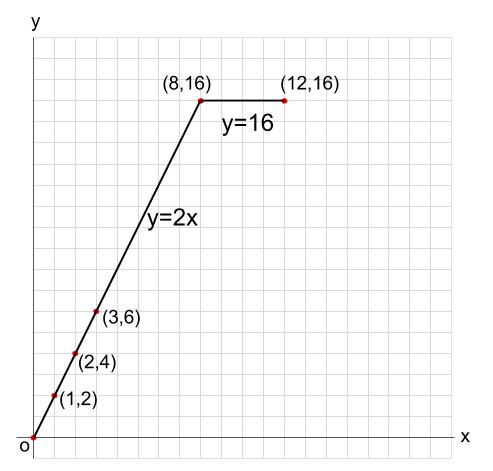
(3)点 \(P\) が \(DA\) 上を動くとき、\(y\) を \(x\) の式で表しなさい。また、\(x\) の変域を求めなさい
点 \(P\) が \(DA\) 間を動くときの図示をしてみましょう。
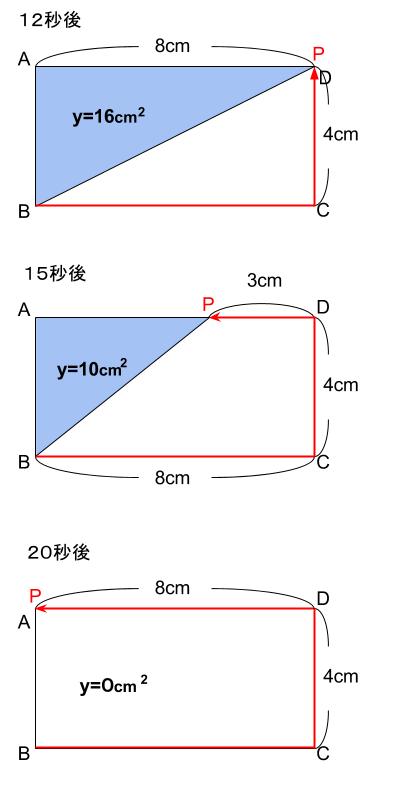
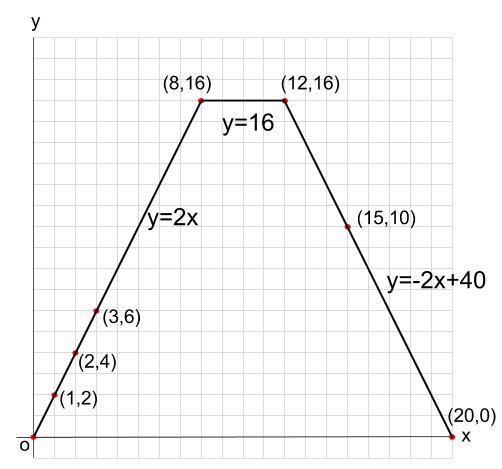
時間とともに、面積が減少していくことがわかりますね。これをグラフにかき足します。
このグラフの式は、\(y=-2x+40\) 、\(12 \leqq x \leqq 20\)です。
式の求め方は大丈夫ですか?直線が通る点が2つわかれば、求められますね。
別解
ちなみに、次のような解法もあります。とても大事ですので必ずこちらも理解しておいてください。
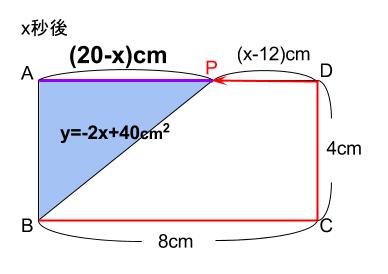
\(x\) 秒後の三角形 \(ABP\) の底辺は、下図の紫色の箇所です。この長さを求めます。
求め方は2通りあります。
解法1
赤+紫を求めます。
この長さは長方形の、よこ、たて、よこの和であり、\(8+4+8=20cm\)です。
赤い長さは、点 \(P\) が \(x\) 秒で動いた距離であり、 \(xcm\) です。
よって、紫の長さは、\(20-x(cm)\) と求まります。
解法2
\(PD\) の長さは、\(x-(8+4)=x-12(cm)\) です。
よって、紫の長さは、\(8-(x-12)=20-x(cm)\) と求まります。
よって、三角形 \(ABP\) の面積 \(y\) は
\(y=(20-x)×4÷2=-2x+40\)
グラフから得た式と、まったく同じ式が得られましたね。
(4)点 \(P\) が \(B\) から \(A\) まで動くとき、\(y\) と \(x\) の関係を表すグラフをかきなさい
グラフはすでに(3)の解説の中で示した通りです。
動点の解法のまとめ
上で学習したことのポイントをまとまめす。
その点を座標平面でとり、直線で結べばいい!!
点から点への途中経過は、一直線に決まっているから!!
これが最速解答です。
つまり、点 \(P\) が各頂点に来たときのみを調べればOKです。
しかし、道中が曲線になる問題も中学3年生以降には出てきますので、
一定の割合で増えているか、減っているか、ある程度調べるくせはつけておきましょうね。
スポンサーリンク
