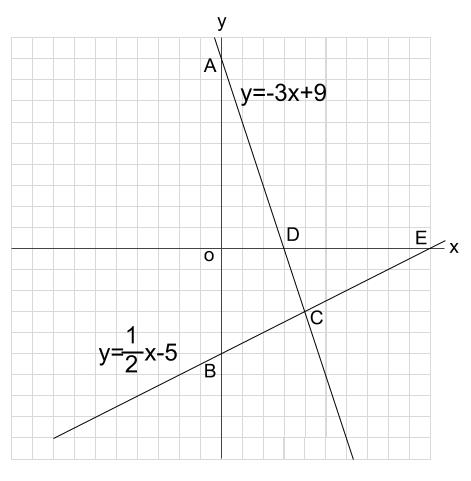
例題1
下の図について、次の問いに答えなさい。
(1)\(A,B,C\) の座標をそれぞれ求めなさい。
(2)\(\triangle ABC\) の面積を求めなさい。
(3)\(\triangle CDE\) の面積を求めなさい。
解説
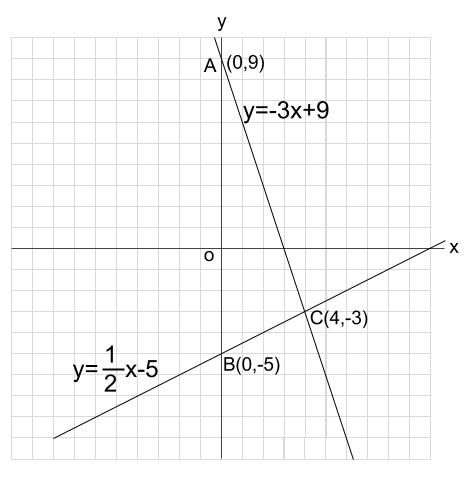
(1)\(A,B,C\) の座標をそれぞれ求めなさい
この問題では、座標の目盛りを数えるだけで求まりますが、計算での求め方を確認しておきましょう。
\(A\) は\(y=-3x+9\) の切片です。つまり、\(x\) 座標が \(0\) で、\(y\) 座標は \(9\) です。
よって、\(A(0,9)\)
\(B\) は\(y=\displaystyle \frac{1}{2}x-5\) の切片です。つまり、\(x\) 座標が \(0\) で、\(y\) 座標は \(-5\) です。
よって、\(B(0,-5)\)
\(C\) は\(2\) 直線、\(y=-3x+9\) と \(y=\displaystyle \frac{1}{2}x-5\) の交点なので、連立方程式を解いて求めます。
$\left\{ \begin{array}{@{}1} y=-3x+9\\ y=\displaystyle \frac{1}{2}x-5 \end{array} \right. $
これを解いて、
$\left\{ \begin{array}{@{}1} x=4\\ y=-3 \end{array} \right. $
よって、\(C(4,-3)\)
問題を解くとき、求まった情報はどんどん図に入れていきます。
パズルを解くためのカギなので、瞬時に使えるように準備することが大事です。
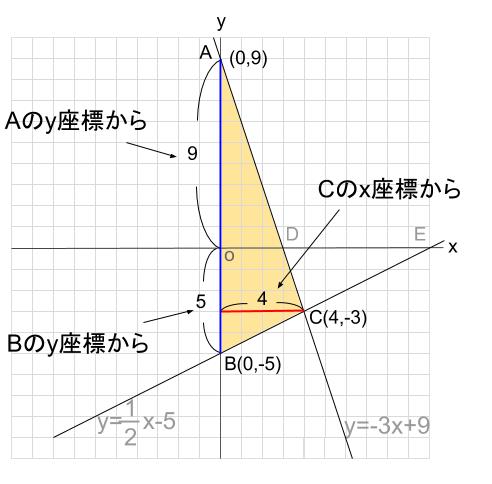
(2)\(\triangle ABC\) の面積を求めなさい
\(A,B,C\) の座標から、\(\triangle ABC\) の底辺の長さ、高さが求まりますね。
下図の青い箇所、\(AB\) を底辺とすれば、その長さは \(A,B\) の \(y\) 座標から得られます。
\(9+5=14\)
高さは、下図の赤色の箇所で、\(C\) の \(x\) 座標より、\(4\)
よってその面積は、\(14×4÷2=28\)
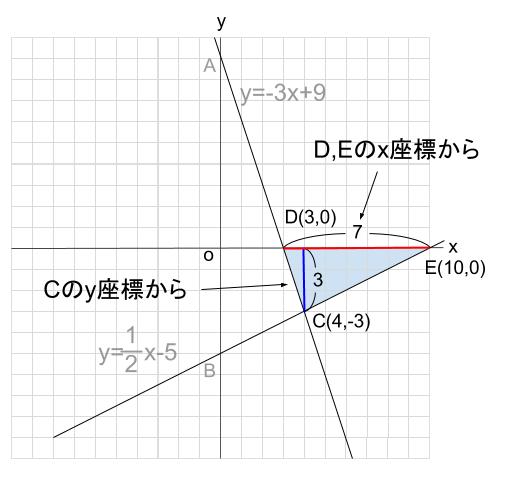
(3)\(\triangle CDE\) の面積を求めなさい
同じく\(D,E\) の座標を求めましょう
\(D\) は\(y=-3x+9\) の、\(y\) 座標が \(0\) の点です。\(y=0\) を直線の式に代入して
\(0=-3x+9\)
\(x=3\)
よって、\(D(3,0)\)
\(E\) は\(y=\displaystyle \frac{1}{2}x-5\) の、\(y\) 座標が \(0\) の点です。\(y=0\) を直線の式に代入して
\(0=\displaystyle \frac{1}{2}x-5\)
\(x=10\)
よって、\(E(10,0)\)
以上から、\(\triangle CDE\) の底辺の長さ、高さが求まりますね。
\(DE\) が底辺ならば、その長さは \(10-3=7\)
高さは、下図の青色の箇所で、\(C\) の \(y\) 座標より \(3\)
よってその面積は、\(7×3÷2=10.5\)
スポンサーリンク
