例題1
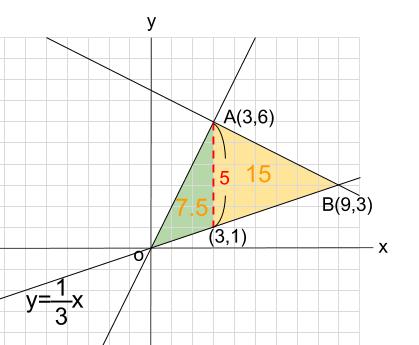
下の図について、\(\triangle AOB\) の面積を求めなさい。
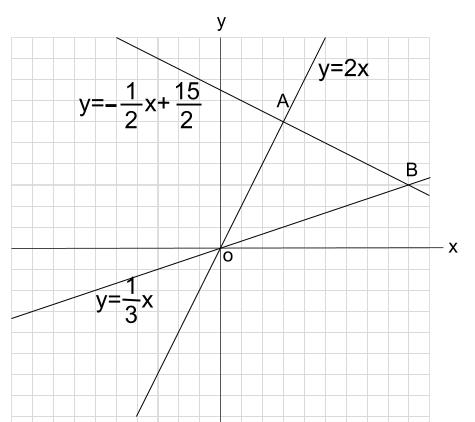
解説
今までと同じように、\(A,B\) の座標を求めましょう。
\(A\) は \(2\) 直線、\(y=2x\) と \(y=-\displaystyle \frac{1}{2}x+\displaystyle \frac{15}{2}\) の交点なので、連立方程式を解いて求めます。
$\left\{ \begin{array}{@{}1} y=2x\\ y=-\displaystyle \frac{1}{2}x+\displaystyle \frac{15}{2} \end{array} \right. $
これを解いて、
$\left\{ \begin{array}{@{}1} x=3\\ y=6 \end{array} \right. $
よって、\(A(3,6)\)
\(B\) は \(2\) 直線、\(y=\displaystyle \frac{1}{3}x\) と \(y=-\displaystyle \frac{1}{2}x+\displaystyle \frac{15}{2}\) の交点なので、連立方程式を解いて求めます。
$\left\{ \begin{array}{@{}1} y=\displaystyle \frac{1}{3}x\\\ y=-\displaystyle \frac{1}{2}x+\displaystyle \frac{15}{2} \end{array} \right. $
これを解いて、
$\left\{ \begin{array}{@{}1} x=9\\ y=3 \end{array} \right. $
よって、\(B(9,3)\)
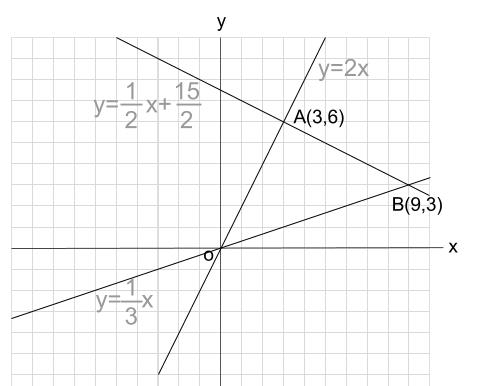
さて、ここから先は何通りもの解法があります。
そのうち代表的ないくつかを紹介していきます。
様々な視点を得ることで、いろいろな問題に対応する力を養ってください。
解法1
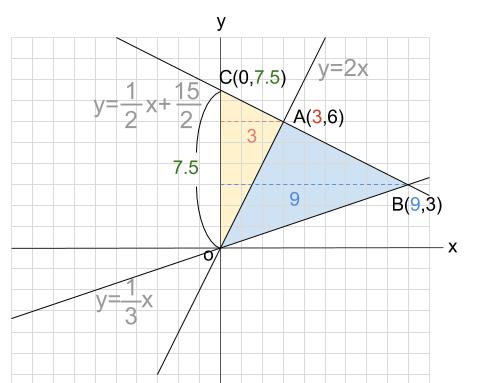
\(y=-\displaystyle \frac{1}{2}x+\displaystyle \frac{15}{2}\) の切片を \(C\) とすると、
この点 \(C\) を利用して、\(大三角形-小三角形\) で求めます。
点 \(C\) の座標は、\(C(0,7.5)\) です。
\(\triangle AOB=\triangle COB-\triangle COA\)
よって、\(7.5×9÷2-7.5×3÷2=22.5\)
解法2
三角形を囲む長方形から、まわりの三角形を引くことでも求められます。
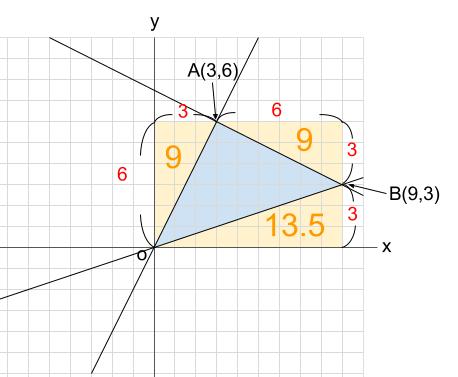
よって、
\(6×9-(9+9+13.5)=22.5\)
解法3
内部底辺と呼ばれるものに着目する方法もあります。
下図の赤線を底辺と見ます。
底辺の長さは \(5\) です。
左の三角形の高さは \(3\)
右の三角形の高さは \(6\)
よって、\(5×(3+6)÷2=22.5\)
スポンサーリンク
