対角線の本数の公式
\(N\) 角形の対角線の本数を求める公式があります。
\(N角形の対角線の本数=(N-3)×N÷2\)
もちろんこの公式は暗記して欲しいのですが、たまにしか利用しない公式なので
よほど熱心に暗記しないと、すぐに忘れてしまいます。
この公式は、「なぜこの公式になるのか」を理解・暗記しましょう。
その方が、「忘れにくい」からです。
無味乾燥な呪文(公式)は、すぐに忘れてしまいますが、
意味のあるストーリーならずっと覚えていられるのです。
公式の導出
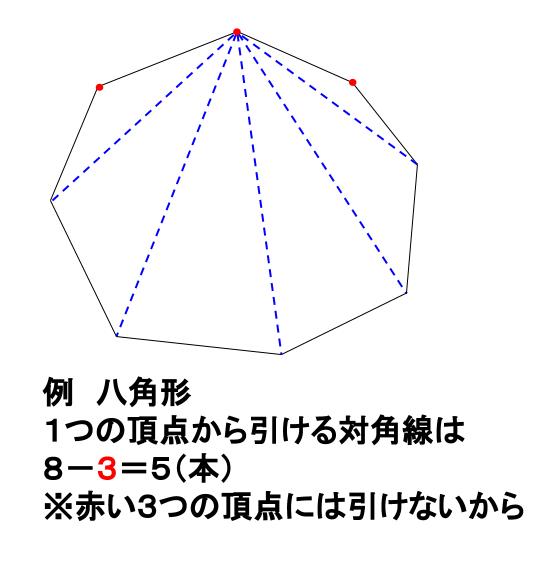
\(N\) 角形の \(1\) つの頂点からひける対角線は何本でしょうか?
\(N-3\) 本です。
自分と、隣りの \(2\) つの頂点、合わせて \(3\) 頂点には、対角線を引くことができません。
\(N\) 個の頂点ですべて、同様に \(N-3\) 本ずつひけるので、
\((N-3)×N\) 本の対角線が引けそうです。
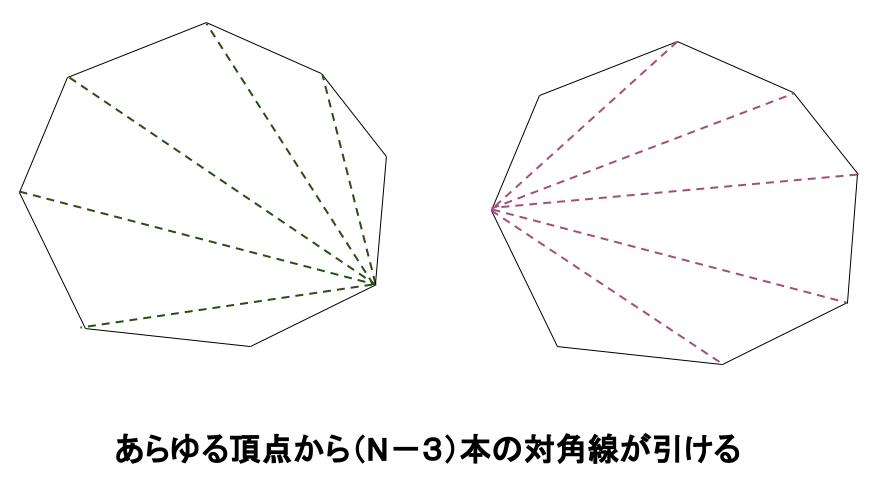
しかし、これではすべての対角線を、\(2\) 回ずつ数えていることになるので、
\((N-3)×N÷2\) が対角線の本数となります。

具体例
いくつか公式を適用して、対角線の本数を求めてみましょう。
五角形・・・\((5-3)×5÷2=5\)
六角形・・・\((6-3)×6÷2=9\)
七角形・・・\((7-3)×7÷2=14\)
八角形・・・\((8-3)×8÷2=20\)
スポンサーリンク
