正三角形
\(3\) つの辺が等しい三角形を正三角形といいます。
正三角形は、二等辺三角形の特別な場合です。
いわば、三等辺三角形です。
正三角形の \(3\) つの内角は等しく、すべて、\(60°\) です。
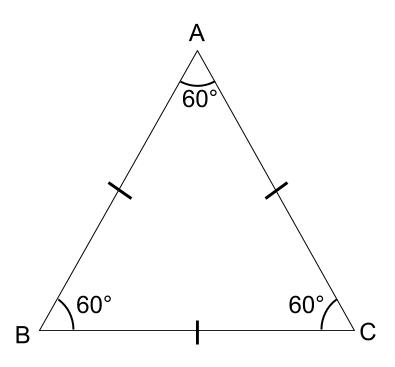
正三角形は線対称な図形である
正三角形は、二等辺三角形なので、二等辺三角形の性質を持っています。
\(AD\) を軸として、正三角形 \(ABC\) は線対称であり、\(BD=CD\) です。
また、三角形 \(ABD\) は三角定規の形の1つです。

※対称の軸は、すべての頂点からひけます。\(3\) 方向すべてが対称的な図形です。
例題1
下の図で、四角形 \(ABCD\) は正方形、三角形 \(DCE\) は正三角形です。 \(\angle x\) の大きさを求めなさい。
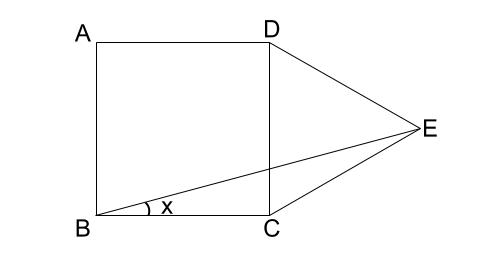
解説
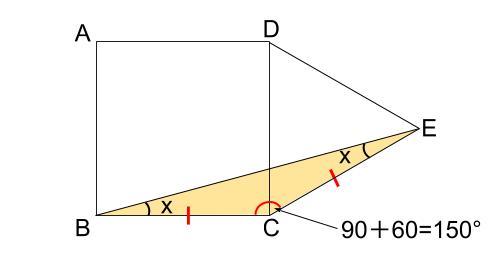
正方形の \(4\) つの辺と、正三角形の \(3\) つの辺がすべて等しい長さなので、
三角形 \(CEB\) が二等辺三角形です。
また、 \(\angle BCE=90°+60°=150°\)
よって、 \(\angle x=(180-150)÷2=15°\)
例題2
下の図で、四角形 \(ABCD\) は正方形、三角形 \(EBC\) は正三角形です。 \(\angle x\) の大きさを求めなさい。
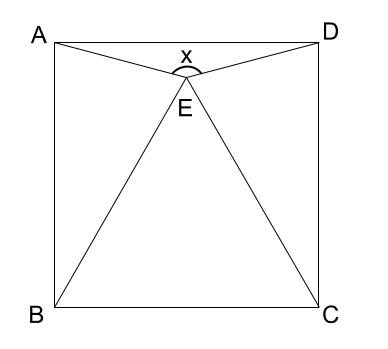
解説
正方形の \(4\) つの辺と、正三角形の \(3\) つの辺がすべて等しい長さなので、
三角形 \(BEA\) が二等辺三角形です。
※もちろん三角形 \(CED\) が二等辺三角形
また、 \(\angle ABE=90°-60°=30°\)
よって、 \(\angle BEA=(180-30)÷2=75°\)
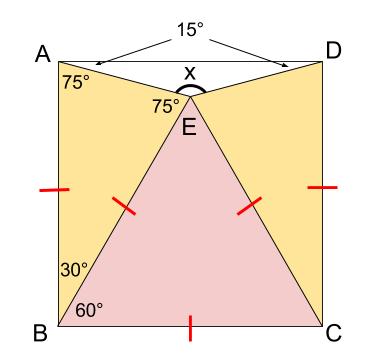
二等辺三角形 \(EDA\) に着目すれば、
\(\angle x=180-15×2=150°\)
あるいは、点 \(E\) の周りの \(4\) つの角に着目すれば、
\(\angle x=360-(75×2+60)=150°\)
スポンサーリンク
