【中学数学】求角・折り返し

折り返した図形

折り返した図においては、折り目の線を対称の軸として
線対称になります。
つまり、折る前と折った後とで、同じ長さ、同じ角度があります。

例題１

下の図は、正三角形 $ABC$ を $DE$ を折り目として折った図で、点 $A$ は点 $A´$ に移動しました。
$\angle x$ の大きさを求めなさい。

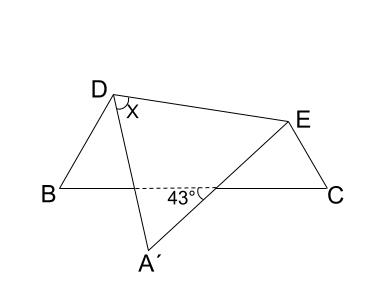
解説

折り返しの問題では、折る前の図を必ず復元しましょう。
はじめから折る前の図が与えられることも多いですが、
ないときは必ず復元します。
等しい角であることを表す記号も入れましょう。

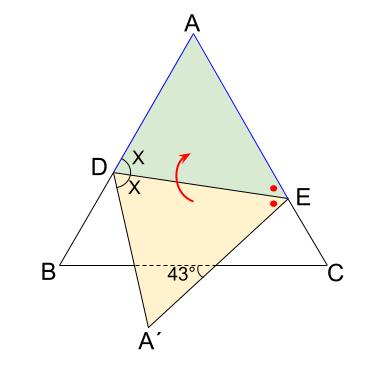
あとは、わかる角を入れていけば、
$\angle x$ にたどりつけるはずです。

下の図で、正三角形の内角は $60°$ です。
オレンジ色の三角形の外角より、赤い角度は
$43+60=103°$
この角は、水色の三角形の外角でもあるので、
紫色の角の大きさは、
$103-60=43°$

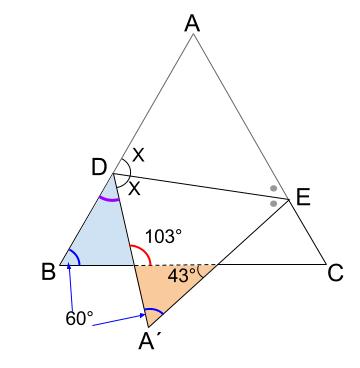
よって、点 $D$ に集まる $3$ つの角の大きさの和が $180°$ なので、
$43+2x=180$
$x=68.5°$

例題２

下の図は、長方形 $ABCD$ を $EF$ を折り目として折った図で、点 $C,D$ はそれぞれ点 $C´,D´$ に移動しました。
$\angle x$ の大きさを求めなさい。

解説

折り返しの問題では、折る前の図を必ず復元します。
等しい角であることを表す記号も入れましょう。

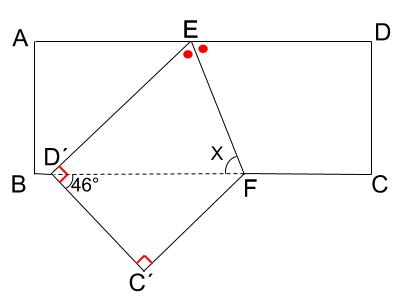
あとは、わかる角を入れていけば、
$\angle x$ にたどりつけるはずです。

下の図で、ピンクの角の大きさは、
$90-46=44°$
また、平行線の錯角は等しいので、
$\angle x$ は、赤丸と等しいです。

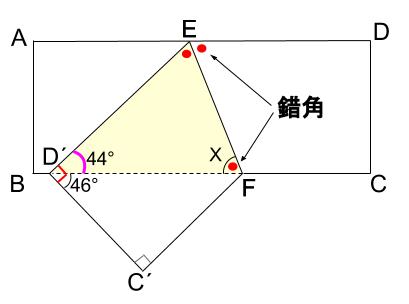
つまり、三角形 $D´FE$ は二等辺三角形になります。
$\angle x=(180-44)÷2=68°$

スポンサーリンク