求角と方程式
角度を求めることは、小学生のころにもやっていることです。
しかし、角度を求めるために方程式を用いることは中学生ならではです。
そんな問題を練習しましょう。
例題1
次の図の角 \(x\) の大きさを求めなさい。
ただし、同じ記号の角は、等しい角の大きさであることを示しています。
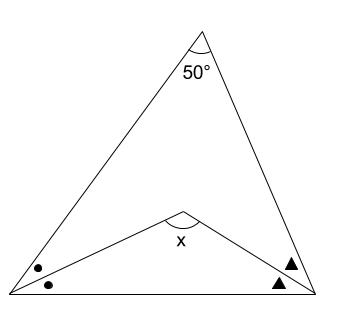
解説
やり方を知っていないと苦戦する問題です。
逆に言えば、一度経験をしてやり方を覚えてしまえば良いだけの問題です。
●や▲は、ただの未知数です。\(y\) や \(z\) と出題されたのと同じことです。
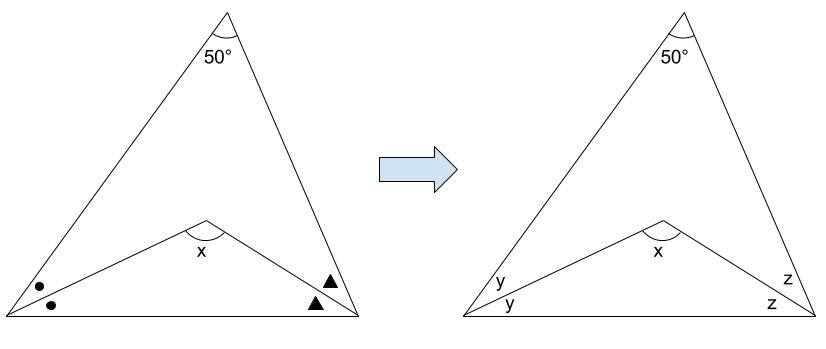
文字なら、「方程式を立式しよう!」ってすぐに思いますよね。
●や▲でも、立式してしまえばいいのです。
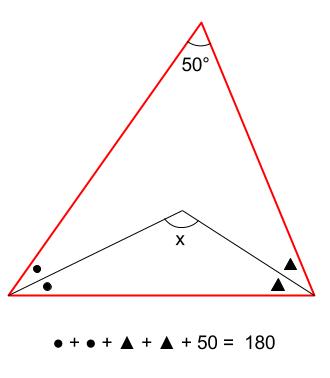
下の図の赤い三角形に着目して 、\((●+▲)×2+50=180\)
より、\(●+▲=65\) ・・・①
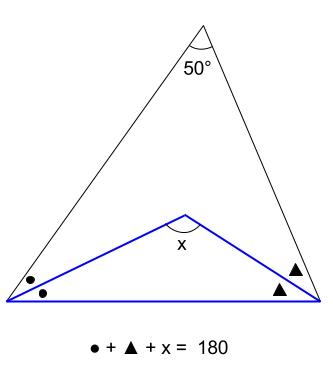
青い三角形に着目して、\(●+▲+x=180\)・・・②
①、②を見比べてみましょう。
\(●+▲=65\) ・・・①
\(●+▲+x=180\)・・・②
\(●+▲=65\) を、②に代入できますね。
\(65+x=180\)
\(x=115°\)
と求まりました。
例題2
次の図の角 \(x\) の大きさを求めなさい。
ただし、同じ記号の角は、等しい角の大きさであることを示しています。
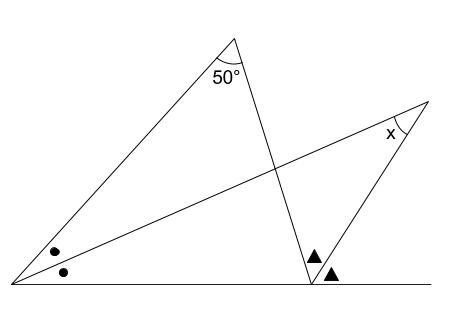
解説
例題1と同様ですね。
立式をしていきましょう。
下の図の赤い三角形に注目すると
\(50+●×2=▲×2\)・・・①
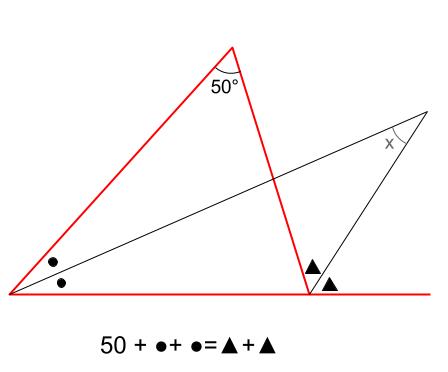
下の図の青い三角形に注目すると
\(x+●=▲\)・・・②
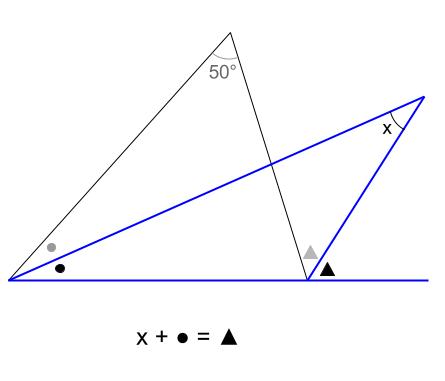
①、②を見比べてみましょう。
\(50+●×2=▲×2\)・・・①
\(x+●=▲\)・・・②
②式を \(2\) 倍すると①式になる!
気付けましたか?
② \(×2\)
\(2x+●×2=▲×2\)・・・② \(×2\)
これを①と見比べると・・・
\(2x=50\)
\(x=25°\)
と求まりました。
参考
②式より、
\(x=▲-●\)・・・③
この▲ー●の値をどうやって得るか・・・
①式を変形することで得られますね。
\(50+●×2=▲×2\)・・・①
\(50=▲×2-●×2\)
この式を \(2\) で割れば
\(25=▲-●\)
つまり、
\(x=25°\)
と求まりました。
まとめ
例題1でも例題2でも、
●や▲の角の大きさは求まりませんでした。
しかし、和(●+▲)や差(▲ー●)を利用することで
角 \(x\) の大きさを求めることができました。
このような式処理もあるということを覚えておきましょう。
スポンサーリンク
