角の和
\(1\) つ\(1\) つの角の大きさではなく、いくつかの角の和を求めよという問題
があります。
\(1\) つ\(1\) つの角の大きさは求まらないことが多く、
角を集めていくことで解決します。
角を集めるためには、三角形の外角を用います。
例題1
下の図で、印をつけた角の大きさの和を求めなさい。

解説
下の図の水色の三角形の外角より、\(2\) つの角の和は、赤い角になります。
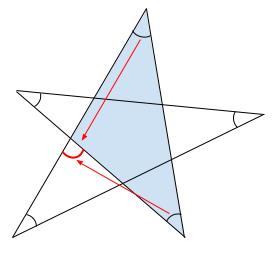
また、下の図のクリーム色の三角形の外角より、\(2\) つの角の和は、青い角になります。
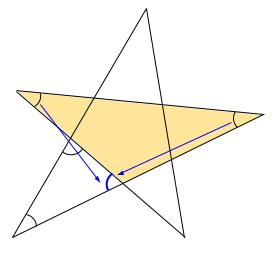
よって、はじめの \(5\) つの角の和は、
下の図の赤い三角形の内角の和と等しいので、\(180°\) と求まります。
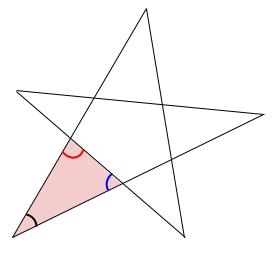
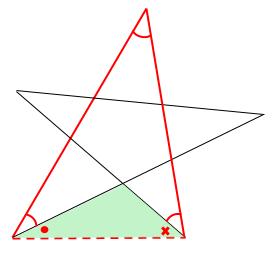
別解
下の図のような補助線を引きます。
クリーム色の三角形の内角 \(2\) つの和は、
緑色の三角形の内角 \(2\) つの和と等しいです。
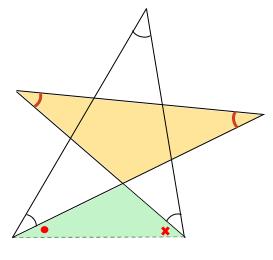
よって、はじめの \(5\) つの角の和は、
下の図の赤い三角形の内角の和と等しいので、\(180°\) と求まります。
例題2
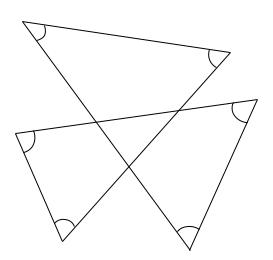
下の図で、印をつけた角の大きさの和を求めなさい。
解説
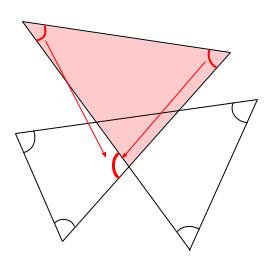
例題1と同様に解けます。
ピンクの三角形の内角 \(2\) つの和が赤い外角と等しい。
水色の三角形の内角 \(2\) つの和が青い外角と等しい。
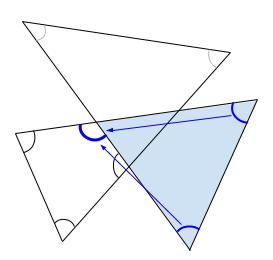
よって、はじめの \(6\) つの角の和は、四角形の内角の和と等しいので、
\(360°\) と求まります。
スポンサーリンク
