直角三角形の合同条件
\(2\) つの直角三角形が合同であることを示したいとき、
以下の \(2\) つを利用します。
直角三角形の合同条件
1 斜辺と \(1\) つの鋭角がそれぞれ等しい。
2 斜辺と他の \(1\) 辺がそれぞれ等しい
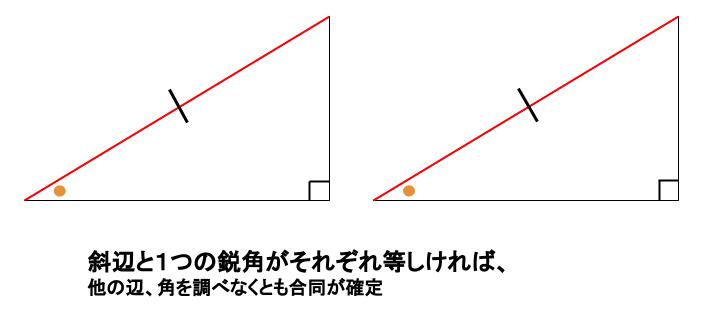
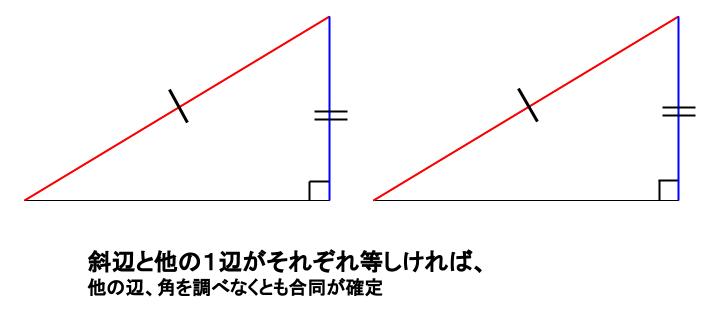
この \(2\) つは暗記してください。
三角形の合同条件 \(3\) つを暗記しましたね?
同じことです、覚えないと話になりません。
斜辺、鋭角
ところで、斜辺、鋭角、という言葉は大丈夫でしょうか?
直角の向かい側の辺が斜辺です。
直角三角形の \(3\) 辺で、最も長い辺が斜辺です。
\(90°\) より小さい角を鋭角といいます。
(\(90°\) より大きい角を鈍角といいます。)
直角三角形の \(3\) つの角は、
\(1\) つは直角、他の \(2\) つは鋭角です。
直角三角形の合同条件をくわしく考察
改めて、直角三角形の合同条件です。
直角三角形の合同条件
1 斜辺と \(1\) つの鋭角がそれぞれ等しい。
2 斜辺と他の \(1\) 辺がそれぞれ等しい
なぜ、この \(2\) つの条件になるのか。
くわしく見てみましょう。
斜辺と \(1\) つの鋭角がそれぞれ等しい
三角形の \(3\) つの角のうち、\(2\) つの角の大きさが等しいならば、
最後に残った角の大きさも等しくなります。
つまり、\(3\) つの角度がすべて同じになります。
これは、斜辺とその両端の角がそれぞれ等しいことになります。
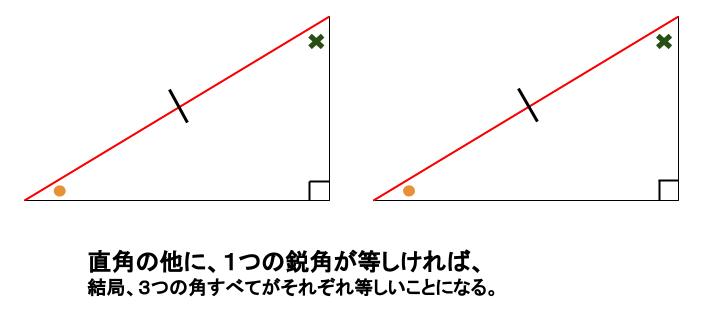
これはつまり、一般の三角形の合同条件の \(1\) つである、
「\(1\) 辺とその両端の角がそれぞれ等しい」
と同じことが成立しているのです。
斜辺と他の \(1\) 辺がそれぞれ等しい
斜辺の長さを \(a\) ,他の \(1\) 辺の長さを \(b\) とします。
長さが \(a,b\) の \(2\) 本の棒を組みあわせて、直角三角形 \(ABC\) を作ります。
ただし、\(\angle ACB=90°\) です。
このとき、直角三角形 \(ABC\) は何通りもつくれるでしょうか?
それとも、ただ \(1\) つに形がきまるでしょうか?
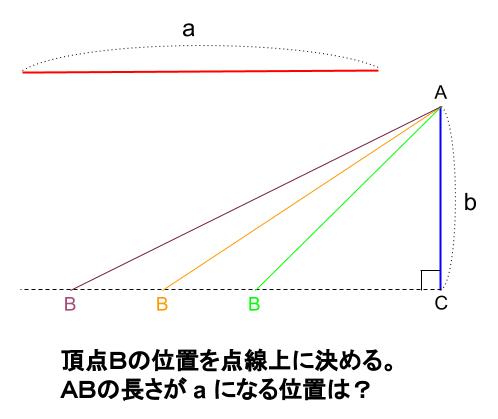
ただ \(1\) つに定まります。
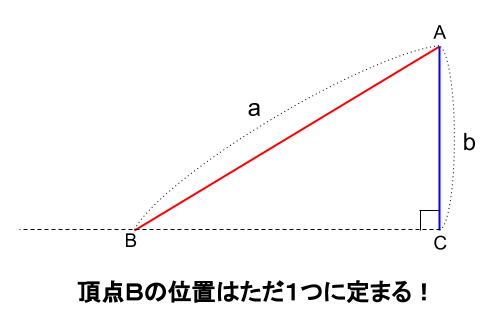
よって、斜辺と他の \(1\) 辺がそれぞれ等しければ、
直角三角形は合同です。
参考
斜辺と他の \(1\) 辺がそれぞれ等しいときに合同であることは、
中学三年生で学習する「三平方の定理」を使えば、成立することは
ものすごく簡単にわかります。
また、中学三年生で学習する「円周角の定理の逆」を使っても、成立することは
ものすごく簡単にわかります。
普通の三角形の合同条件を用いてよい
\(2\) つの直角三角形の合同を示したいときに、
普通の三角形の合同条件を用いてもかまいません。
直角三角形も、当然ですが三角形なのですから。
