平行四辺形の性質
証明の問題に、平行四辺形がでてくることがあります。
このとき、平行四辺形には以下の \(4\) つが成り立っていることは
暗黙の前提です。証明なしで使って構いません。
・\(2\) 組の対辺がそれぞれ平行
・\(2\) 組の対辺がそれぞれ等しい
・\(2\) 組の対角がそれぞれ等しい
・対角線がそれぞれの中点で交わる
例題1
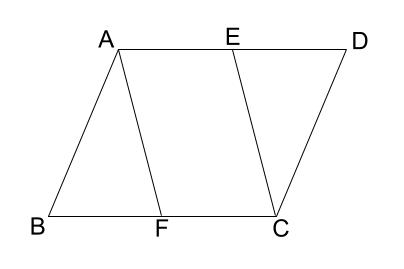
下の図で、、平行四辺形 \(ABCD\) の辺 \(AD,BC\) 上に \(ED=FB\) となる点 \(E,F\) をとる。
このとき、\(AF=CE\) となることを証明しなさい。
解説
線分の長さが等しいことを示したいとき、
示すための根拠の第一候補は、その線分を含む三角形の合同でしたね。
\(AF,CE\) を含む三角形は、\(\triangle ABF , \triangle CDE\) です。
見た感じでも \(\triangle ABF \equiv \triangle CDE\) ですね。
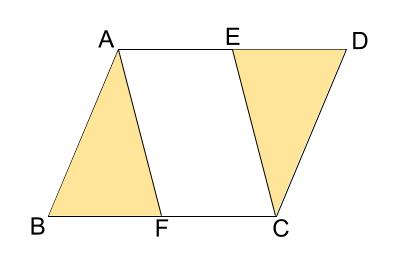
本当に合同なのか、等しい辺、角を入れていきましょう。
仮定より \(BF=DE\)
平行四辺形の対辺なので、 \(AB=CD\)
平行四辺形の対角なので、 \(\angle ABF=\angle CDE\)
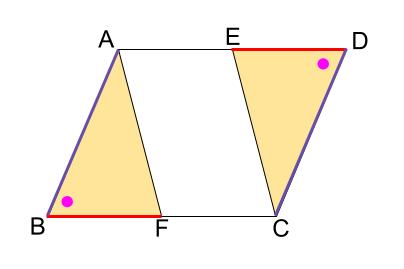
\(2\) 辺とその間の角が等しいですね。
これを証明にまとめます。
※ほとんど上の文そのままの証明になりますね。
解答
\(\triangle ABF\) と \(\triangle CDE\) において
仮定より \(BF=DE\) ・・・①
平行四辺形の対辺なので、 \(AB=CD\) ・・・②
平行四辺形の対角なので、 \(\angle ABF=\angle CDE\) ・・・③
①、②、③より \(2\) 辺とその間の角が等しいから
\(\triangle ABF \equiv \triangle CDE\)
合同な図形の対応する辺の長さは等しいので
\(AF=CE\)
例題2
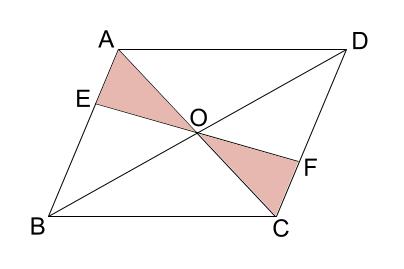
下の図で、、平行四辺形 \(ABCD\) の対角線 \(AC,BD\) の交点を \(O\) とし、 \(O\) を通る直線と辺 \(AB,CD\) との交点をそれぞれ \(E,F\) とする。このとき、\(AE=CF\) となることを証明しなさい。
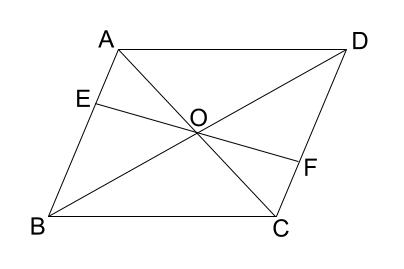
解説
線分の長さが等しいことを示したいので、上と同様です。
\(AE,CF\) を含む三角形は、\(\triangle AEO , \triangle CFO\) です。
本当に合同なのか、等しい辺、角を入れていきましょう。
平行四辺形の対角線は中点で交わるので、 \(OA=OC\)
平行線の錯角なので、 \(\angle OAE=\angle OCF\)
対頂角なので、 \(\angle EOA=\angle FOC\)
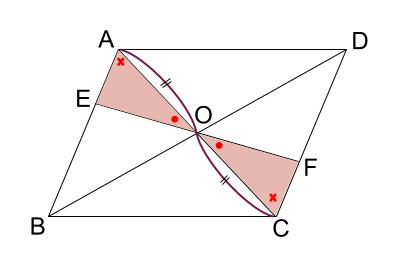
\(1\) 辺とその両端の角が等しいですね。
これを証明にまとめます。
解答
\(\triangle AEO\) と \(\triangle CFO\) において
平行四辺形の対角線は中点で交わるので、 \(OA=OC\) ・・・①
平行線の錯角なので、 \(\angle OAE=\angle OCF\) ・・・②
対頂角なので、 \(\angle EOA=\angle FOC\) ・・・③
①、②、③より \(1\) 辺とその両端の角が等しいから
\(\triangle AEO \equiv \triangle CFO\)
合同な図形の対応する辺の長さは等しいので
\(AE=CF\)
