例題1
平行四辺形 \(ABCD\) の辺 \(AB,BC,CD,DA\) の中点をそれぞれ \(E,F,G,H\) とします。
線分 \(AG,EC\) と線分 \(HB\) との交点をそれぞれ \(P,Q\) とし、
線分 \(AG,EC\) と線分 \(DF\) との交点をそれぞれ \(S,R\) とするとき、
四角形 \(PQRS\) は平行四辺形であることを証明しなさい。

解説
平行四辺形になるための \(5\) 条件を暗記し、
どれに該当するのか、探っていきます。
辺の長さ、角の大きさが等しいことを示すのはかなり難しそうです。
もちろん対角線もあらかじめ与えられていません。
残っているのは
・\(2\) 組の対辺がそれぞれ平行
です。
下図の \(2\) つが平行四辺形であることを示せば、
「\(2\) 組の対辺がそれぞれ平行」と言えます。
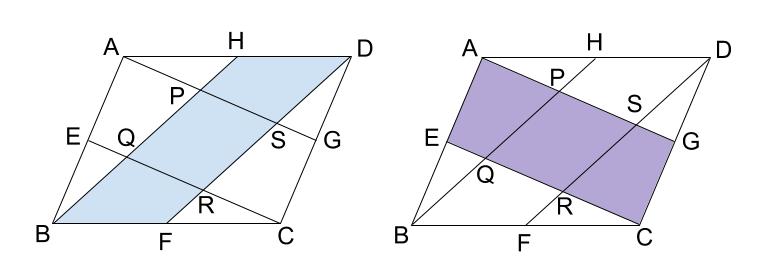
どちらも、
「\(1\) 組の対辺が平行でその長さが等しい」ことから、
平行四辺形であると示せます。
解答
四角形 \(ABCD\) が平行四辺形なので、\(HD /\!/ BF\) ・・・①
四角形 \(ABCD\) が平行四辺形なので、\(AD = BC\) ・・・②
仮定より点 \(H,F\) は中点なので、これと②より
\(HD=BF\) ・・・③
①、③より、\(1\) 組の対辺が平行で、その長さが等しいので、
四角形 \(HBFD\) は平行四辺形である。
同様に四角形 \(AECG\) も平行四辺形である。
平行四辺形 \(HBFD\) の対辺なので、\(PQ /\!/ SR\) ・・・④
平行四辺形 \(AECG\) の対辺なので、\(PS /\!/ QR\) ・・・⑤
④、⑤より、\(2\) 組の対辺がそれぞれ平行なので、
四角形 \(PQRS\) は平行四辺形である。
例題2
平行四辺形 \(ABCD\) の辺 \(AB,BC,CD,DA\) の中点をそれぞれ \(E,F,G,H\) とします。
このとき、四角形 \(EFGH\) は平行四辺形であることを証明しなさい。
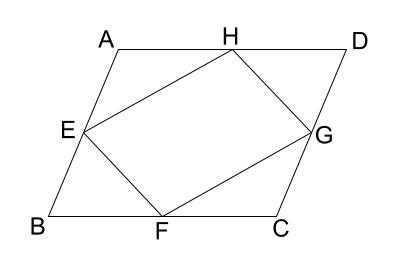
解説
平行四辺形になるための \(5\) 条件のどれに該当するのか。
辺の長さ、角の大きさ、対辺が平行であること・・・
どれを示すことができそうしょうか?
とりあえず、下のクリーム色の三角形の合同を示すことで、
\(FE=HG\) がいえます。
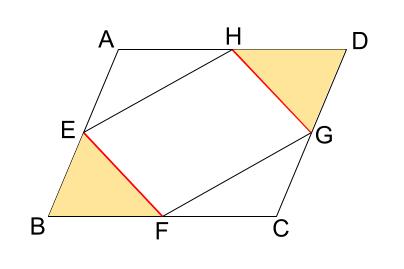
さらに 平行 \(FE /\!/ HG\) が言えれば、「\(1\) 組の対辺が平行で、その長さが等しい」
なのですが・・・
平行であることを示すためには、
同位角か錯角が等しいことを言わないとなりません。
例えば下図の錯角が等しいことを言えそうでしょうか。
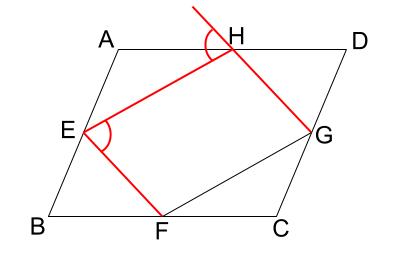
なかなか難しそうです。
簡単には言えなそうですね。
もう \(1\) 組の三角形の合同から解決します。
下の紫色の三角形の合同を示すことで、
\(EH=GF\) が言えます。
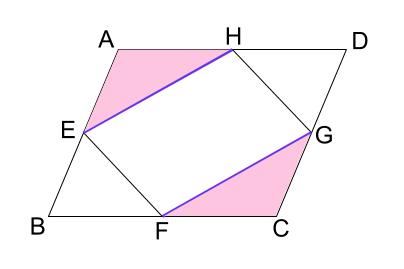
つまり、\(2\) 組の対辺がそれぞれ等しいから
四角形 \(EFGH\) は平行四辺形であると言えます。
解答
\(\triangle EBF\) と \(\triangle GDH\) において
四角形 \(ABCD\) が平行四辺形なので、\(AD = BC\) ・・・①
仮定より点 \(H,F\) は中点なので、これと①より
\(HD=BF\) ・・・②
四角形 \(ABCD\) が平行四辺形なので、\(AB = DC\) ・・・③
仮定より点 \(E,G\) は中点なので、これと③より
\(EB=GD\) ・・・④
四角形 \(ABCD\) が平行四辺形なので、\(\angle EBF=\angle GDH\) ・・・⑤
②、④、⑤より、\(2\) 辺とその間の角それぞれ等しいので、
\(\triangle EBF \equiv \triangle GDH\)
合同な図形の対応する辺の長さは等しいので、
\(FE = HG\) ・・・⑥
同様に \(\triangle AEH \equiv \triangle CGF\) であり
合同な図形の対応する辺の長さは等しいので、
\(EH = GF\) ・・・⑦
⑥、⑦より、\(2\) 組の対辺がそれぞれ等しいので、
四角形 \(EFGH\) は平行四辺形である。
