平行四辺形になるための条件
四角形 \(ABCD\) が平行四辺形であることを示せ。
このような問題を学習していきます。
四角形 \(ABCD\) が平行四辺形であることを示すためには、
以下の \(5\) つのうち、どれか \(1\) つが成り立てばよいのです。
・\(2\) 組の対辺がそれぞれ平行
・\(2\) 組の対辺がそれぞれ等しい
・\(2\) 組の対角がそれぞれ等しい
・対角線がそれぞれの中点で交わる
・\(1\) 組の対辺が平行で、その長さが等しい
なんと \(5\) つもありますが・・・
しっかり覚えてください。
よく用いるのは
・対角線がそれぞれの中点で交わる
・\(1\) 組の対辺が平行で、その長さが等しい
の \(2\) つです。
まずはこの \(2\) つをしっかり覚えましょう。
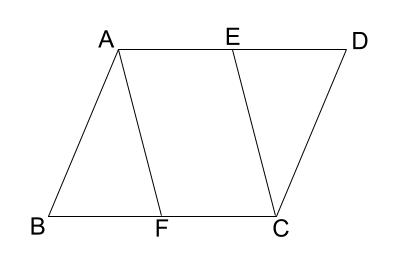
例題1
平行四辺形 \(ABCD\) の辺上に点 \(E,F\) を、 \(DE=BF\) となるようにとる。
このとき、四角形 \(AFCE\) は平行四辺形であることを証明しなさい。
解説
平行四辺形になるための \(5\) 条件を暗記し、
どれに該当するのか、探っていきます。
上で書いた通り、まず候補とすべきなのが
・対角線がそれぞれの中点で交わる
・\(1\) 組の対辺が平行で、その長さが等しい
の \(2\) つです。
この問題では、示すべき四角形 \(AFCE\) の対角線はないので、
・対角線がそれぞれの中点で交わる
は除外しましょう。
※自ら対角線を引いて、それが中点で交わることを示すことは、ほぼないです。
絶対ないと言ってしまってよいくらいです。
この問題では、
・\(1\) 組の対辺が平行で、その長さが等しい
が成り立ちますね。
\(AE /\!/ FC\)
\(AE=FC\)
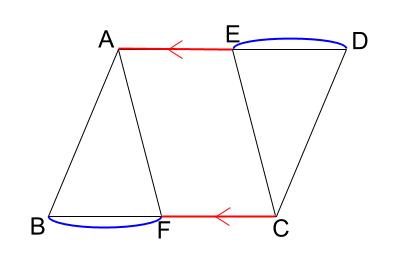
これを解答としてまとめます。
解答
四角形 \(ABCD\) が平行四辺形なので、\(AE /\!/ FC\) ・・・①
四角形 \(ABCD\) が平行四辺形なので、\(AD = BC\) ・・・②
仮定より、 \(DE=BF\) ・・・③
②、③より、
\(AD-DE=BC-BF\)
よって、\(AE=FC\)・・・④
①、④より、\(1\) 組の対辺が平行で、その長さが等しいので、
四角形 \(AFCE\) は平行四辺形である。
参考・三角形の合同の証明の利用
下の図のように、
\(\triangle ABF \equiv \triangle CDE\)
を証明し、\(FA=CE\) をいうことができます。
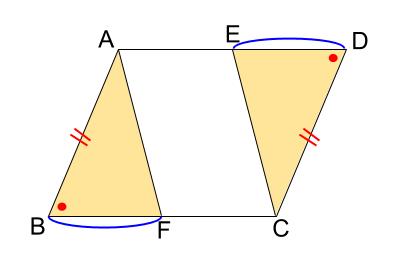
これと \(AE=FC\)
から、\(2\) 組の対辺がそれぞれ等しいから四角形 \(AFCE\) は平行四辺形である
という証明の流れも可能です。
証明の解答には別解がありうることは知っておいてください。
例題2
平行四辺形 \(ABCD\) の対角線の交点を \(O\) とし、対角線 \(AC\) 上に
点 \(E,F\) を \(AE=CF\) となるようにとる。
このとき、四角形 \(EBFD\) は平行四辺形であることを証明しなさい。
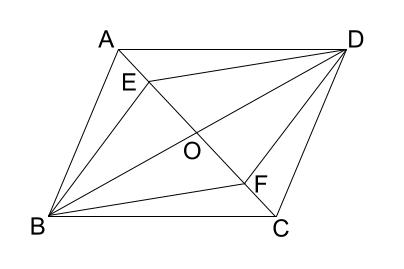
解説
対角線が与えられていますから、
・対角線がそれぞれの中点で交わる
から示せそうです。
実際に、それで正解です。
対角線があらかじめ与えられているときは、ほぼ間違いなく
・対角線がそれぞれの中点で交わる
から証明することになります。
覚えておきましょう。
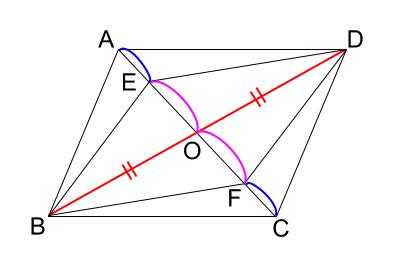
解答
四角形 \(ABCD\) が平行四辺形なので、\(BO=DO\) ・・・①
四角形 \(ABCD\) が平行四辺形なので、\(AO = CO\) ・・・②
仮定より、 \(AE=CF\) ・・・③
②、③より、
\(AO-AE=CO-CF\)
よって、\(EO=FO\)・・・④
①、④より、対角線がそれぞれの中点で交わるので、
四角形 \(EBFD\) は平行四辺形である。
