合同を証明せよ
証明の導入問題
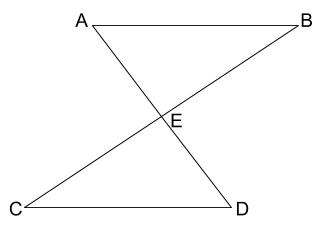
下図において、\(BC\) の中点を \(E\) 、\(AB /\!/ CD\)であるとき、
\(\triangle ABE \equiv \triangle DCE\) であることを証明せよ。
証明??なにそれ?
このような、「合同を証明せよ」という、人生ではじめてのことを学習していきます。
証明とはどのようにしたらよいのでしょうか。
そもそも \(2\) つの三角形は本当に合同なのでしょうか。
「三角形の合同の証明」とは、
この \(2\) つの大きなハードルを乗り越える必要があります。
\(2\) つをまとめて解決しようとするのは下手なやり方です。
\(1\) つずつ学習していきましょう。
このページでは、
「そもそも \(2\) つの三角形は本当に合同なのか」
これに焦点を当てていきます。
三角形の合同条件といいます。合同であることの確かめ方についてです。
「証明とはどのようにしたらよいのか」については次回に持ち越します。
はたして2つの三角形は合同なのか
見た感じは似ていますね。合同な気がします。
しかし、完全に同じ三角形なのかと言われると・・・
数学では、「見た感じ同じだから」のような曖昧な議論は許されません。
論理で説明できないといけません。
\(2\) つの三角形の「\(3\) つの辺と \(3\) つの角がそれぞれ等しい」と与えられれば、その \(2\) つの三角形は合同に決まってます。
しかし、上の例題で、\(3\) つの辺と \(3\) つの角がそれぞれ等しいとは言えません。
そんなにたくさんの情報は与えられていませんから・・・
しかし、もっともっと少ない情報量で、\(2\) つの三角形の合同を示すことができるのです。
三角形の合同条件
\(2\) つの三角形が合同になるために、最低限これだけの情報が必要なんだ!
これが三角形の合同条件です。
三角形の合同条件は \(3\) つあります。
- \(3\) 辺がそれぞれ等しい
- \(2\) 辺とその間の角がそれぞれ等しい
- \(1\) 辺とその両端の角がそれぞれ等しい
この \(3\) つのうち、いずれか \(1\) つを満たせば、\(2\) つの三角形は合同といえます。
なにはともあれ、丸暗記をして下さい。
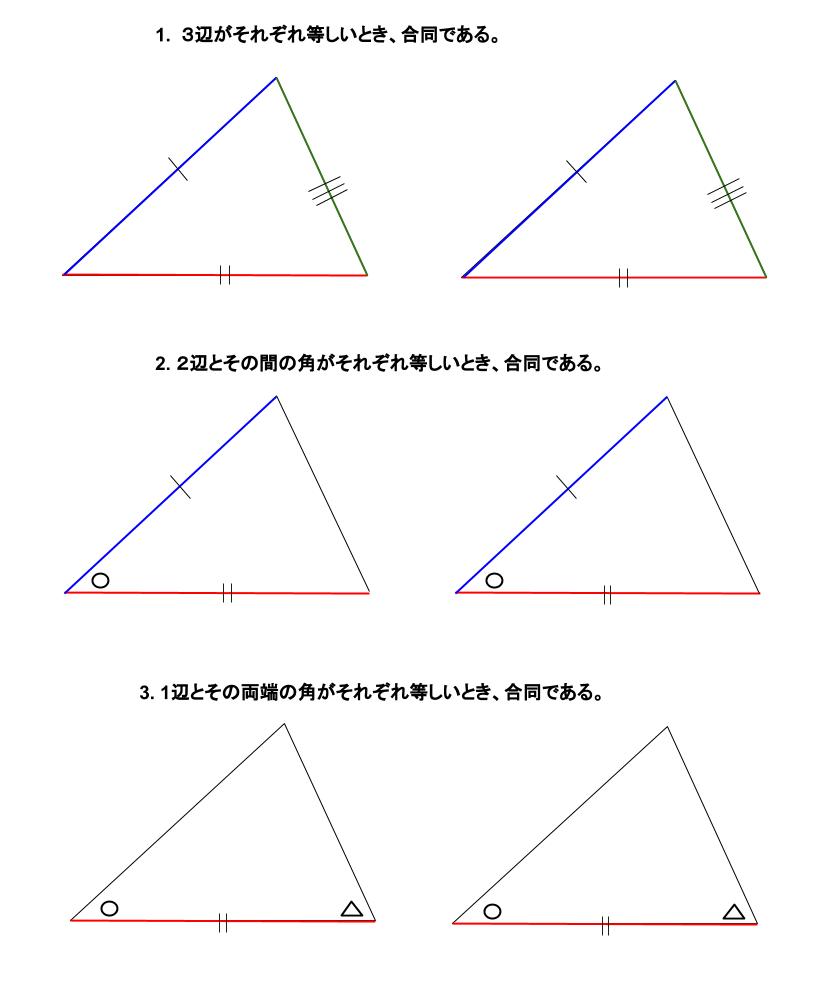
改めて強調しますが、この \(3\) つの「三角形の合同条件」は暗記してください。
絶対に!!
しかし、なんでこの条件になるのかな?
という疑問を持ち、それに対して納得をしておきたい気持ちも大事です。
以下で、合同条件は他にないのか。
もっと少ない情報では合同が確定しないのか、などを考察してみましょう。
1つの辺が等しい。角度についての条件はなし
\(2\) つの三角形があって、どちらも \(1\) 辺は \(10cm\) で等しいんだ。
これだけの情報では、\(2\) つの三角形が合同であるとは確定できませんね。

「\(1\) つの辺が等しい」だけでは、合同が確定するためには、条件が少なすぎます。
2つの辺がそれぞれ等しい。角度についての条件はなし
三角形の \(3\) 辺のうち、1辺は \(10cm\)、もう\(1\) 辺は \(9cm\)、あと \(1\) 辺の長さはわからないんだけどね・・・
そんな三角形が \(2\) つあるんだ。
これだけの情報では、\(2\) つの三角形が合同であるとは確定できませんね。

「\(2\) つの辺がそれぞれ等しい」だけでは、合同が確定するためには、条件が少なすぎます。
3つの辺がそれぞれ等しい。角度についての条件はなし
三角形の \(3\) 辺のうち、\(1\) 辺は \(10cm\)、もう\(1\) 辺は \(9cm\) 、もう \(1\) 辺は \(6cm\) なんだ。
そんな三角形が \(2\) つあるんだ。
この情報では、\(2\) つの三角形が合同であると確定します!
ただ \(1\) 種類の三角形しか作れません。
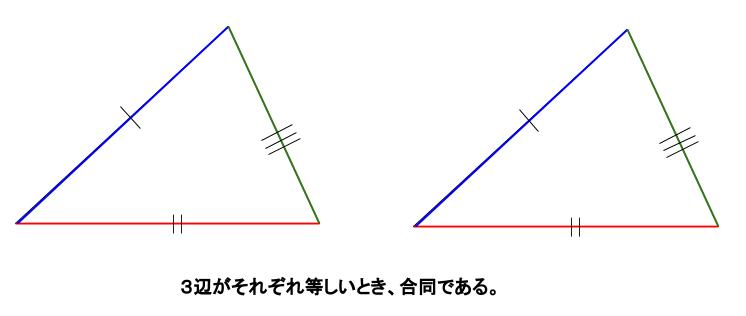
\(3\) 辺がそれぞれ等しい
これは合同条件の \(1\) つといえます。
1辺と、その両端の角がそれぞれ等しい
では、角度の条件を与えてみましょう。
「\(1\) つの辺が等しい」だけでは合同条件にはならなかったので、さらに角度が等しいという条件も与えてみます。
どれだけ少ない角度で大丈夫でしょうか?
いろいろ図示して考えてみると・・・
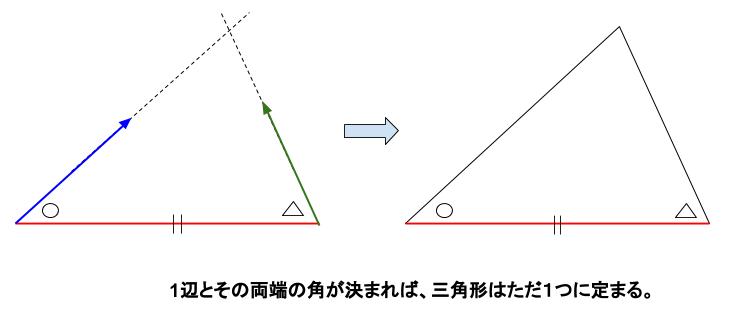
「\(1\) 辺と、その両端の角がそれぞれ等しい」で確定します。
実は角度の情報は、その場所も指定しなくてはいけません。
2辺と、その間の角がそれぞれ等しい
さらに、「\(2\) つの辺が等しい」だけでは合同条件にはならなかったので、角度の情報を与えてみます。
どれだけ少ない角度で大丈夫でしょうか?
いろいろ図示して考えてみると・・・
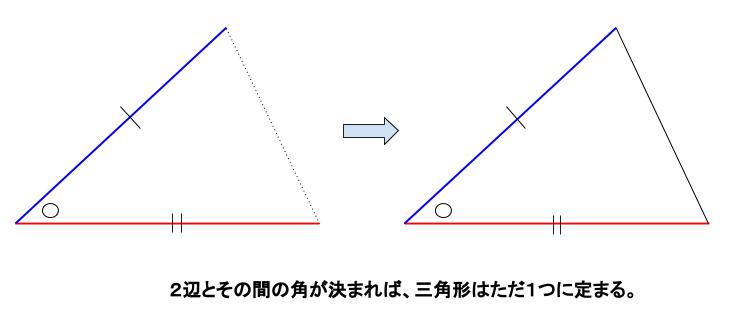
「\(2\) 辺と、その間の角がそれぞれ等しい」で確定します。
今回も角度の情報は、その場所も指定しなくてはいけません。
三角形の合同条件 まとめ
このように、さまざまな条件で、合同が確定するかどうかを調べていくと、
今まででてきた \(3\) つが、三角形の合同条件のすべてであることがわかります。
※みなさんは、この結果を受け入れて、しっかりと暗記しましょう。
三角形の合同条件は \(3\) つです。いずれも、辺と角、あわせて \(3\) つの情報が必要です。
- \(3\) 辺のみ \(3\) 辺がそれぞれ等しい
- \(2\) 辺と \(1\) 角 \(2\) 辺とその間の角がそれぞれ等しい
- \(1\) 辺と \(2\) 角 \(1\) 辺とその両端の角がそれぞれ等しい
例題
\(3\) つの角の大きさがそれぞれ、\(30°,70°,80°\) の三角形をかいて下さい。
ただし、\(1\) 辺の長さは \(5cm\) です。
この指示に従って、\(P\) くんと \(Q\) くんの \(2\) 人が三角形をかきました。
\(2\) 人のかいた三角形は必ず合同になると言えるだろうか。
解答
三角形の合同条件を \(3\) つ覚えましたか?
これらのいずれかにあてはまるかどうか考えれば・・・
あてはまりませんね。
ですので、必ず合同になるとは言えません。
※偶然同じになる可能性はあります。
以上で解決、と言っても良いのですが、図示して厳密に考えてみましょう。
もし合同になるのならば、
「\(3\) つの角と \(1\) つの辺の長さがそれぞれ等しい三角形は合同である」
と言えるわけですが・・・
図示して考えてみてくださいね。
\(P\) くん、 \(Q\) くんのかいた三角形は以下の \(3\) 通りが考えられます。
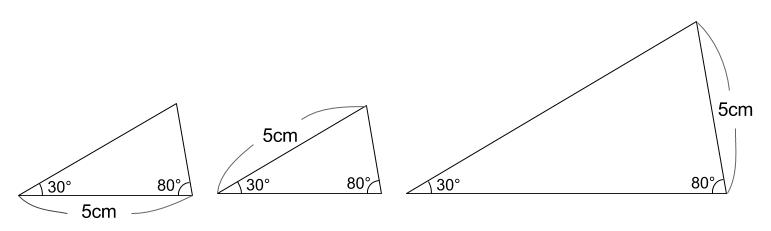
つまり、ただ \(1\) つの三角形に定まらないのです。
だから、「\(3\) つの角と \(1\) つの辺の長さがそれぞれ等しい三角形は合同である」は成り立ちません。
※ちなみに、上図の \(3\) つの三角形はコピー機で縮小・拡大をした関係になっています。そっくりな形です。
これを「相似」といい、中学3年生で学習します。
