例題
下図において、\(BC\) の中点を \(E\) 、\(AB /\!/ CD\)であるとき、
\(\triangle ABE \equiv \triangle DCE\) であることを証明せよ。
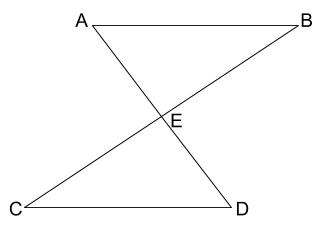
解説
さて、いよいよ「証明をする」という段階に入っていきます。
この問題では、与えられた \(2\) つの三角形が合同であると証明せよ、というのです。
ですので、「合同なのか合同ではないのかの判定」をするのではありません。
合同なんです。
合同である、という結論は与えてもらっています。
ただし、その根拠をきちんと示してね、という問題なのです。
初心者がいきなりこの証明問題の解答をかけないのは普通のことです。
どのように書いていくべきなのか、そもそも何を解答すればよいのか。
\(1\) ステップずつ段階を踏んで身につけていきましょう。
証明を書くということの中には、多くの要素が詰まっているため、いきなり全部をこなそうとしてもなかなかなかなか苦しいものです。
証明を書くとは大きく分けると下のような \(2\) 段階です。
- 証明すべきことが、自分でわかること
- それを論理立ててかくこと
たったの \(2\) 段階ともいえますが、
2、論理立てて書く
もいきなりはできないでしょう。
このパートも細分化して見ていきます。
安心してついてきてください!
ステップ1 まず自分がわかること。
まず、本当に \(2\) つの三角形は合同なのか、自分がわかる必要があります。
わからないことを人に説明することができませんからね。
よって、まず自分が理解しないことにははじまりません。
本当に\(\triangle ABE \equiv \triangle DCE\) は成り立っているのでしょうか?
とうやって確かめたらよいのでしょうか。
それはもちろん、合同条件です。
\(2\) つの三角形が \(3\) つの合同条件のどれかを満たすことを確かめるのです。
長さと角の大きさの情報を図に入れる
合同条件は、辺の長さと角の大きさが話題です。
よって、等しい辺、等しい角をチェックします。
図に入れていきましょう。
これは大事な下準備です。
\(BC\) の中点を \(E\) ⇒ \(BE\) と \(CE\) の長さが等しい
\(AB /\!/ CD\)
この \(2\) つを図に入れます。
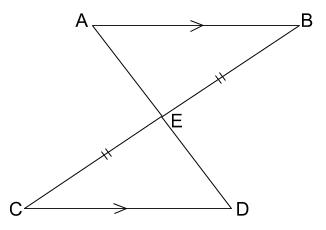
平行は、角の大きさが等しいことに使う
三角形の合同条件に、平行であるかどうか、という条件はありません。
平行は、角度に使用します。
平行線の同位角、錯角は等しいからです。
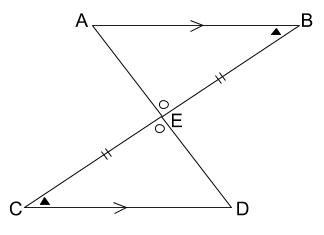
これで、三角形の合同条件のいずれかを満たしているか、順に探します。
「\(1\) 辺とその両端の角がそれぞれ等しい」ですね。
これで、\(2\) つの三角形が合同であることが確かめられました。
次に、いま確かめたことを、他人に一から説明するための文を書いていきます。
ステップ2 形式に則って、証明文をかく
証明文のおおまかな流れが以下のようになることはご理解いただけますね。
——————————————————————————————————

\(BE=CE\)・・・①
角○が等しい・・・②
角▲が等しい・・・③
①②③より、\(\triangle ABE \equiv \triangle DCE\)
——————————————————————————————————
これにきちんと肉づけをしていきます。
まず大事なことは、角○が等しい、とは本当なのか?
という根拠が必要です。
なぜ辺の長さは等しいといえるのか、なぜ角の大きさが等しいといえるのか、
これらには、きちんとその理由を付け加えないといけません。
それに、 角○ という表記もダメです。
これは、設計図をかいたときの自分だけにわかる記号です。
他人に伝わるように、ていねいに証明文をかかなくてはなりません。
ではどのように書けば良いのか。
下の例文で学習しましょう。
——————————————————————————————————

仮定より、\(BE=CE\)・・・①
対頂角なので、\(\angle BEA=\angle CED\)・・・②(角○が等しいを正式にかくと)
平行線の錯角は等しいので、\(\angle ABE\)=\(\angle DCE\)・・・③(角▲が等しいを正式にかくと)
①②③より、\(\triangle ABE \equiv \triangle DCE\)
——————————————————————————————————
①仮定より、BE=CE
まず、①の理由です。
\(BE=CE\) は、問題文ですでに与えられていることです。
ですので論理的に証明する必要のないことです。
このように、問題文ではじめから与えられた条件については、
「仮定より」という言葉をつければOKです。
日常で使わない言葉ですので、とにかく慣れましょう。
「仮定より」は「問題文ではじめから条件として与えられた前提なので」
と同じ意味です。
②対頂角なので、\(\angle BEA=\angle CED\)
○の角が等しいことの説明です。
「対頂角なので」という理由をつけます。
③平行線の錯角は等しいので、\(\angle ABE\)=\(\angle DCE\)
▲の角が等しいことの説明です。
「平行線の錯角が等しいので」という理由をつけます。
この証明文でほぼOKです。
この文を読んで、\(2\) つの三角形がなぜ合同なのか、人に伝わることでしょう。
しかしこれではまだ不完全なのです。
ステップ3 宣言文と合同条件を提示する
どこか不完全なのか。
ずばり、
証明の形式に則った書き方をしていない
という点です。
証明の形式に則るために、いくらか文章を付け足します。
次に付け足す文章は、ただのルール(規則)と思ってもらって結構です。
次の解答が、模範解答例になります。
【模範解答例】
——————————————————————————————————
\(\triangle ABC\) と \(\triangle DEF\) において(←この宣言文をつける)
仮定より、\(BE=CE\)・・・①
対頂角なので、\(\angle ABE\)=\(\angle DCE\)・・・②
平行線の錯角は等しいので、\(\angle ABE\)=\(\angle DCE\)・・・③
①②③より、\(1\) 辺とその両端の角が等しいので、
(←合同条件をのどれを適用したのかつける。)
\(\triangle ABE \equiv \triangle DCE\)
——————————————————————————————————
\(\triangle ABC\) と \(\triangle DEF\) において
\(\triangle ABC\) と \(\triangle DEF\) において
まず、宣言文で注目をさせます。
これから何について証明をするのか、読む側に準備をさせる文章と言えます。
これをつけるのがルールです。あまり深く考える必要はありません。
①②③より、1辺とその両端の角が等しいので
そして、結論の \(1\) つ前に、必ず合同条件をかきます。
「\(1\) 辺とその両端の角が等しいので」の部分です。
この合同条件をかかないと、
1 なぜ合同なのか説明しきれていない
とも言えますし
2 読む人にとって不親切
とも言えます。
これについても、あまり深く考えないで、ルールだから、と思ってもらって結構です。
以上で、\(2\) つの三角形の合同を証明することができました!!
まとめ 三角形の合同の証明
大まかな流れは以下のようになります。
——————————————————————————————————
三角形~と三角形~ において、
合同条件にあてはまる等しい辺か角を理由とともに示す・・・①
合同条件にあてはまる等しい辺か角を理由とともに示す・・・②
合同条件にあてはまる等しい辺か角を理由とともに示す・・・③
①、②、③より、「三角形の合同条件の \(3\) つうちのどれか」なので、
三角形~ ≡ 三角形~
——————————————————————————————————
この型にはまりましょう!
