例題1
下の図で \(AB=AE\)、\(AC=AD\) のとき \(\triangle ABC \equiv \triangle AED\) となることを証明しなさい。
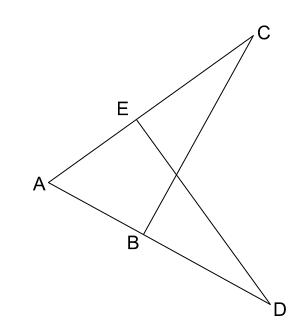
解説
まずは下準備です。
仮定(はじめから与えられた条件)を図に入れましょう。
このとき、辺の長さが等しい という条件を図に入れたいのですが、
辺が重なっていて、どれとどれが等しいのか一目でわかるように図示できません。
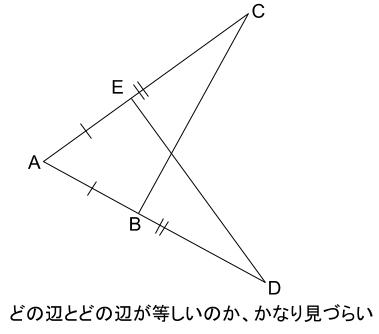
よって、以下のようなマーキングをおすすめします。
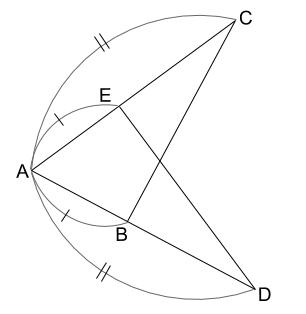
さて、三角形の合同条件を探ります。
現在、示したい三角形の \(2\) 辺の長さがそれぞれ等しいことがわかっています。
あと \(1\) 辺の長さが等しい
か、あるいは、
間の角が等しいことを言えれば、
三角形の合同条件にあてはまります。
このように、
三角形の合同条件を知っていて、
あと何が言えれば合同条件にあてはまるのか、
という逆算の視点で問題を見るのです。
合同条件を知らないで合同を示すことなどできません。
今回は、すでに等しいとわかっている \(2\) 辺の間の角が等しいことがいえます。
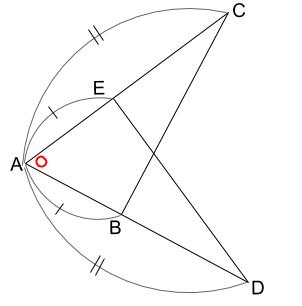
ところで、この赤丸の角が等しいことについて、
理由はなんと書けばいいのでしょうか。
等しいなんて当たり前じゃん・・・って思いますよね。
これは、
共通な角なので、
とい理由をかきます。
※「共通なので」でもOKです。
これで準備が整いました。
解答
\(\triangle ABC\) と \(\triangle AED\) において
仮定より \(AB=AE\)
仮定より \(AC=AD\)
共通なので、\(\angle CAB=\angle DAE\)
よって、\(2\) 辺とその間の角がそれぞれ等しいので
\(\triangle ABC \equiv \triangle AED\)
このようになります。
