正三角形
正三角形とは、\(3\) つの辺が等しい三角形です。
よって問題に正三角形が与えられたら、\(3\) つの辺が等しいことは仮定になります。
また、正三角形の \(1\) つの内角が \(60°\) であること、\(3\) つの内角が等しいことも、
証明なしで使ってかまいません。
例題1
下の図で、\(\triangle ABC\) と \(\triangle ADE\) は正三角形である。このとき、\(\triangle ABD \equiv \triangle ACE\) であることを証明しなさい。
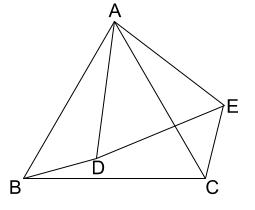
解説
正方形が \(2\) つある図での証明問題は前にやりました。
それと非常にそっくりな問題です。
まずは \(\triangle ABD\) と \(\triangle ACE\) が合同であることを確かめます。
この \(2\) つの三角形の
辺が等しい
角が等しい
を探して、図にいれます。
正三角形の \(3\) つの辺は等しいので、
\(AB=AC\) ・・・赤い箇所、正三角形\(ABC\) より
\(DA=EA\) ・・・青い箇所、正三角形\(ADE\) より
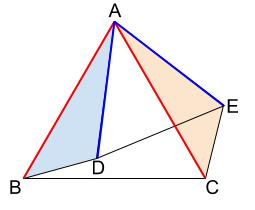
\(2\) 辺が等しいまでわかったので、
残りは、
最後の \(1\) 辺が等しい
\(2\) 辺の間の角が等しい
のどちらかを言えるはずです。
どちらなのか考えてみてください。
今回は、角度の方です。
正三角形の \(1\) つの内角は \(60°\) です。
下図で、
青+赤\(=60°\)・・・正三角形\(ABC\) の内角
紫+赤\(=60°\)・・・正三角形\(ADE\) の内角
この \(2\) つを合わせて、青=紫 です。
どちらも、\(60°-\)赤 です。
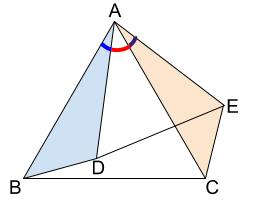
これで、\(\triangle ABD \equiv \triangle ACE\) であることが確かめられました。
これを証明の文章にまとめます。
解答
\(\triangle ABD\) と \(\triangle ACE\) において、
仮定より、\(AB=AC\)・・・①
仮定より、\(DA=EA\)・・・②
また、\(\angle DAB=\angle CAB- \angle CAD=60°- \angle CAD \)・・・③
また、\(\angle EAC=\angle EAD- \angle CAD=60°- \angle CAD \)・・・④
③、④より、
\(\angle DAB=\angle EAC\) ・・・⑤
①、②、⑤より
\(2\) 辺とその間の角がそれぞれ等しいので
\(\triangle ABD \equiv \triangle ACE\)
例題2
下の図で、\(\triangle ABC\) と \(\triangle CDE\)は正三角形である。このとき、\(DA=EB\) であることを証明しなさい。
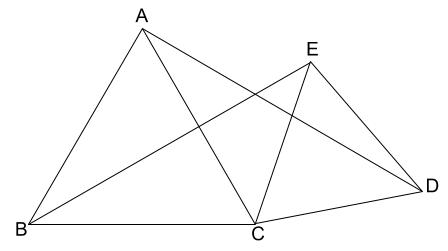
解説
\(DA\) と \(EB\) を辺とする三角形の合同を示すのですね!
\(\triangle ACD \equiv \triangle BCE\)
が目標になります。
等しい辺、角は下のようになります。
赤い辺は、\(\triangle ABC\) が正三角形
青い辺は、\(\triangle CDE\) が正三角形
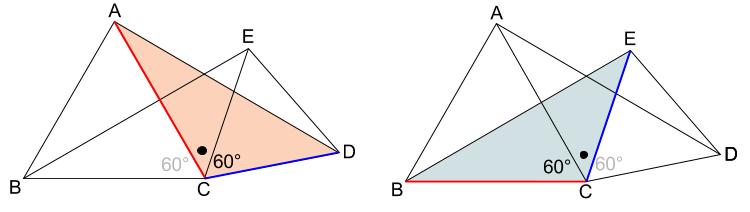
\(2\) 辺とその間の角がそれぞれ等しいことから合同がいえます。
解答
\(\triangle ACD\) と \(\triangle BCE\) において、
仮定より、\(AC=BC\)・・・①
仮定より、\(CD=CE\)・・・②
また、\(\angle ACD=\angle ACE+ \angle ECD=\angle ACE+60° \)・・・③
また、\(\angle BCE=\angle ACE+ \angle BCA=\angle ACE+60° \)・・・④
③、④より、
\(\angle ACD=\angle BCE\) ・・・⑤
①、②、⑤より
\(2\) 辺とその間の角がそれぞれ等しいので
\(\triangle ACD \equiv \triangle BCE\)
合同な図形の対応する辺の長さは等しいので、\(DA=EB\)
まとめ
\(2\) つの正三角形が、\(1\) つの頂点を共有している図が頻出です。
パターンは \(2\) つしかありません。
・\(2\) つの正三角形が重なっている(例題1)
・\(2\) つの正三角形が重なっていない(例題2)
このときの「\(2\) つの三角形の合同の証明」は、ほぼ同じ流れになりますが、
\(2\) つの辺の間の角が等しいことを示す箇所だけ微妙に異なります。
・\(2\) つの正三角形が重なっているとき
\(60°-同じ角度\) で示します。
・\(2\) つの正三角形が重なっていないとき
\(60°+同じ角度\) で示します。
