合同とは
\(2\) つの図形がまったく同じ形、同じ大きさであるとき、
その \(2\) つの図形は合同であるといいます。
まったく同じ形、同じ大きさ、という言葉はけっこう曖昧なので、
厳密にはもっと堅苦しい表現で合同は定義されます。
しかし、直感的に合同がわかってもらえればOKです。
例えば下の図の四角形 \(ABCD\) と四角形 \(HEFG\) は合同です。
四角形 \(ABCD\) ≡ 四角形 \(HEFG\)
と表します。
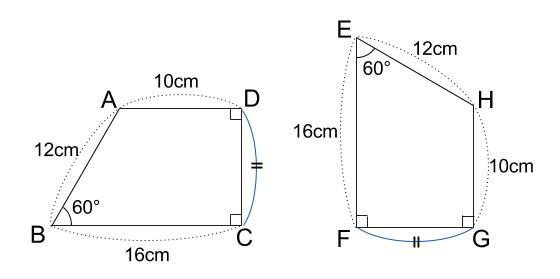
\(2\) つの四角形の紙があると思ってください。
この紙を手に持って重ねたときに、ピタッと重なる図形が合同です。
裏返しでも合同
裏返した図形でも合同です。
※鏡像といいます。
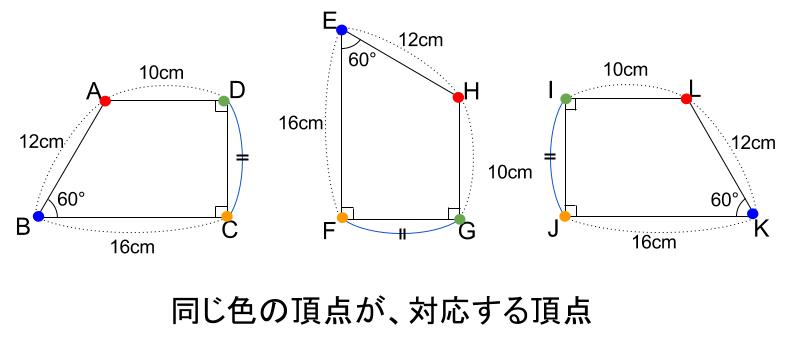
下の図の四角形 \(LKJI\) も、四角形 \(ABCD\) と合同です。
四角形 \(ABCD\) ≡ 四角形 \(LKJI\)

合同な図形の対応する頂点、辺、角
合同な図形を、ピッタリ重ねたときに、重なる頂点、辺、角をそれぞれ
対応する頂点
対応する辺
対応する角
といいます。
合同な図形は、対応する頂点の順番をそろえて表すことが求められます。
つまり、
四角形 \(ABCD\) ≡ 四角形 \(HEFG\)
四角形 \(ABCD\) ≡ 四角形 \(LKJI\)
が正しく、
四角形 \(ABCD\) ≡ 四角形 \(EFGH\) とか
四角形 \(ABCD\) ≡ 四角形 \(IJKL\) ではいけません。
安易にアルファベット順に並べればよいわけではないので注意してください。
合同な図形の性質
①対応する線分の長さはそれぞれ等しい
「対応する線分」とは、ピタッと重ねたときに重なる辺どうしのことです。
その長さが等しいなんて、あたりまえとしか言いようがありませんね・・・
下の図で、\(CD=FG\) です。
これも対応する頂点の順にかきます。
\(CD=GF\) ではいけません。
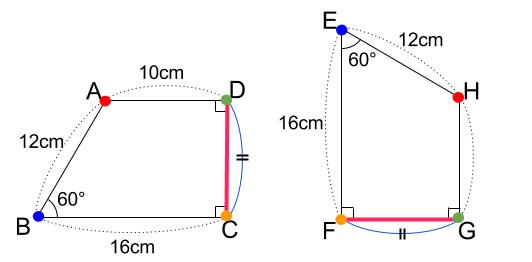
※ちなみに、\(CD,FG\) の長さは、中学3年生で習いますが、\(6\sqrt{3}\) です。
②対応する角の大きさはそれぞれ等しい
「対応する角」とは、ピタッと重ねたときに重なる角どうしのことです。
その大きさが等しいなんて、あたりまえとしか言いようがありませんね・・・
下の図で、\(\angle DAB=\angle GHE \) です。
これも対応する頂点の順にかきます。
\(\angle DAB=\angle EHG\) ではいけません。
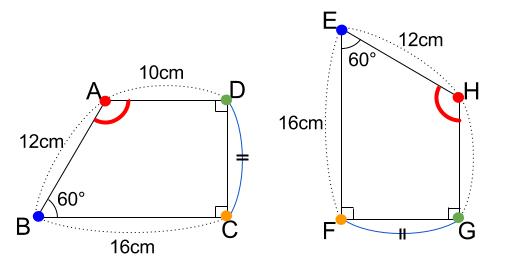
※もちろん、\(\angle DAB=\angle GHE=120° \) です。
